Question

利用平行线的性质探究： 如图，直线AC∥BD，连接AB，直线AC，BD及线段AB把平面分成①②③④四个部分，规定线上各点不属于任何部分．当动点P落在某个部分时，连接PA、PB，构成∠PAC、∠APB、∠PBD三个角．当动点P落在第①部分时，小明同学在研究∠PAC、∠APB、∠PBD三个角的数量关系时，利用图1，过点P作PQ∥BD，得出结论：∠APB＝∠PAC＋∠PBD请你参考小明的方法解决下列问题： (1)当动点P落在第②部分时，在图2中画出图形，写出∠PAC、∠APB、∠PBD三个角的数量关系； (2)当动点P落在第③、第④部分时，在图3、图4中画出图形，探究∠PAC、∠APB、∠PBD之间的数量关系，写出结论并选择其中一种情形加以证明．

Answer 1

答案：
解析：

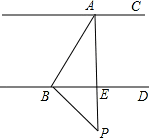
解：(1)如图，当动点P落在第②部分时，∠APB＝360°－(∠PAC＋∠PBD)； 　　(2)当动点P落在第③部分时，∠PAC＝∠APB＋∠PBD； 　　当动点P落在第④部分时，∠PAC＝∠APB＋∠PBD 　　证明：如图，∵∠PAC＝∠AEB， 　　∠AEB＝∠PBD＋∠APB， 　　∴∠PAC＝∠APB＋∠PBD