Question

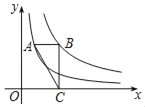
【题目】如图，抛物线经过三点．点是抛物线段上一动点（不含端点，与的延长线交于点

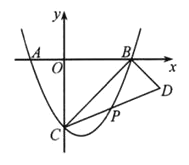
（1）求抛物线的解析式．

（2）当时，求点的坐标。

（3）在（2)的条件下，求的面积．

Answer 1

【答案】（1）抛物线解析式为；（2）点的坐标是；（3）.

【解析】

（1）利用待定系数法求出解析式即可.

（2）连接，根据直角三角形斜边的中线等于斜边的一半，可得，根据“”可证≌，可得，即得点在第四象限角平分线上，可设点的坐标为．()，将点代入抛物线解析式中，可得 ，求出即可.

（3）由于，可得，由，根据三角形的面积公式代入计算即可.

（1）解：∵抛物线经过轴上的点，．解析式为．

将代入，得

即 ,解得，．

∴抛物线解析式为

（2）解：连接

∵，, ∴．

∵,,

∴≌ ()．

∴

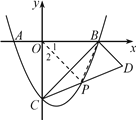
∴点在第四象限角平分线上．

∴可设点的坐标为．()

∴

∴

∴．

∴点的坐标是；

（3）解：∵, ∴ ．

∴．

∵，

．

∴．

∴.

故答案为：（1）抛物线解析式为；（2）点的坐标是；（3）.