题目内容
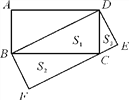
【题目】如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1__ __S2+S3;(填“>”“=”或“<”)
(2)写出图中的三对相似三角形,并选择其中一对进行证明.
【答案】△BCD∽△CFB,△BCD∽△DEC,△CFB∽△DEC
【解析】试题分析:(1)根据S1=![]() S矩形BDEF,S2+S3=
S矩形BDEF,S2+S3=![]() S矩形BDEF,即可得出答案.
S矩形BDEF,即可得出答案.
(2)根据矩形的性质,结合图形可得:△BCD∽△CFB∽△DEC,选择一对进行证明即可.
试题解析:
(1) ∵S1=![]() BD×ED,S矩形BDEF=BD×ED,
BD×ED,S矩形BDEF=BD×ED,
∴S1=![]() S矩形BDEF,
S矩形BDEF,
∴S2+S3=![]() S矩形BDEF,
S矩形BDEF,
∴S1=S2+S3.
△BCD∽△CFB,△BCD∽△DEC,△CFB∽△DEC.
(2)△BCD∽△CFB∽△DEC.
证明△BCD∽△DEC;
证明:∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°,
∴∠EDC=∠CBD,
又∵∠BCD=∠DEC=90°,
∴△BCD∽△DEC.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目