题目内容
【题目】如图，在等腰三角形ABC中，AC=BC，分别以BC和AC为直角边向上作等腰直角三角形△BCD和△ACE，AE与BD相交于点F，连接CF并延长交AB于点G．求证：CG垂直平分AB．
【答案】证明见解析．
【解析】试题分析：通过证明△AFC≌△CEB可得∠ACF=∠BCF，根据等腰三角形三线合一的性质即可得．
试题解析：∵CA=CB，
∴∠CAB=∠CBA，
∵△AEC和△BCD为等腰直角三角形，
∴∠CAE=∠CBD=45°，∠FAG=∠FBG，
∴∠FAB=∠FBA，
∴AF=BF，
在三角形ACF和△CBF中，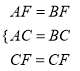 
，
∴△AFC≌△BCF（SSS），
∴∠ACF=∠BCF，
∴AG=BG，CG⊥AB（三线合一），
即CG垂直平分AB.
练习册系列答案
名校课堂系列答案
相关题目
