��Ŀ����
����Ŀ����֪���ھ���ABCD�У�AB��4 cm��BC��8 cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO.
(1)��ͼ�٣�����AF��CE����˵���ı���AFCEΪ���Σ�����AF�ij���
(2)��ͼ�ڣ�����P��Q�ֱ��A��C����ͬʱ�������ء�AFB�͡�CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У���֪��P���ٶ�Ϊ5 cm/s����Q���ٶ�Ϊ4 cm/s���˶�ʱ��Ϊt s������A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��

���𰸡���1��AF��5 cm����2��t��![]() .
.
�������������������1��������֪������֤OA��OC��OE��OF�����ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��������ж��ı���AFCEΪƽ���ı���������EF��AC�����ݶԽ����ഹֱ��ƽ���ı���Ϊ���Σ������ж��ı���AFCEΪ��������AF��CF��x cm����BF��(8��x)cm����Rt��ABF�У����ݹ��ɶ����г����̣��ⷽ�����x��ֵ���������AF�ij�����2����P����AF�ϣ�Q����CD��ʱ��A��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�ͬ��P����AB�ϣ�Q����DE��CE��ʱ��Ҳ�����ܹ���ƽ���ı��Σ����ֻ�е�P����BF�ϣ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ���ͼ������AP��CQ������A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���ʱPC��QA����t��ʾ��PC��QA�ij����г�������t����.
���������
(1)���ı���ABCD�Ǿ��Σ�
��AD��BC.
���CAD����ACB����AEF����CFE.
��EF��ֱƽ��AC������ΪO��
��OA��OC.
���AOE�ա�COF.
��OE��OF.
���ı���AFCEΪƽ���ı��Σ�
����EF��AC��
���ı���AFCEΪ���Σ�
��AF��CF��x cm����BF��(8��x)cm��
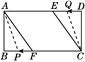
��Rt��ABF�У�AB��4 cm���ɹ��ɶ�����42��(8��x)2��x2�����x��5.
��AF��5 cm.
(2)��Ȼ��P����AF�ϣ�Q����CD��ʱ��A��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�ͬ��P����AB�ϣ�Q����DE��CE��ʱ��Ҳ�����ܹ���ƽ���ı��Σ����ֻ�е�P����BF�ϣ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ���ͼ������AP��CQ������A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���ʱPC��QA.����P���ٶ�Ϊ5 cm/s����Q���ٶ�Ϊ4 cm/s���˶�ʱ��Ϊt s��
��PC��5t cm��QA��(12��4t)cm.��5t��12��4t�����t��![]() .
.
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��t��![]() .
.

 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�