题目内容
三角形的三个外角之比为2:2:3,则此三角形为
- A.锐角三角形
- B.钝角三角形
- C.直角三角形
- D.等边三角形
A
分析:因为三角形的三个外角之比为2:2:3,可以设一个外角是2x°,那么其他两个外角一定是2x°,3x°,根据三角形外角和定理,三个外角的和是360°,就可列方程求解.
解答:设一个外角是2x°,那么其他两个外角一定是2x°,3x°.
根据题意列方程,得2x°+2x°+3x°=360°,
解得x=(51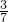 )°,
)°,
则三个外角分别是: 度,
度, 度,
度, 度.
度.
与这三角相邻的三个内角分别是: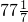 度,
度,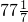 度,
度, 度.
度.
因为都是锐角,所以此三角形是锐角三角形.
故选A.
点评:本题考查三角形外角的性质及三角形的外角和定理,实际上证明了三角形的外角和是360°,解答的关键是沟通外角和内角的关系.
分析:因为三角形的三个外角之比为2:2:3,可以设一个外角是2x°,那么其他两个外角一定是2x°,3x°,根据三角形外角和定理,三个外角的和是360°,就可列方程求解.
解答:设一个外角是2x°,那么其他两个外角一定是2x°,3x°.
根据题意列方程,得2x°+2x°+3x°=360°,
解得x=(51
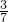 )°,
)°,则三个外角分别是:
 度,
度, 度,
度, 度.
度.与这三角相邻的三个内角分别是:
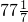 度,
度,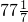 度,
度, 度.
度.因为都是锐角,所以此三角形是锐角三角形.
故选A.
点评:本题考查三角形外角的性质及三角形的外角和定理,实际上证明了三角形的外角和是360°,解答的关键是沟通外角和内角的关系.

练习册系列答案
相关题目
三角形的三个外角之比为2:2:3,则此三角形为( )
| A、锐角三角形 | B、钝角三角形 | C、直角三角形 | D、等边三角形 |