题目内容
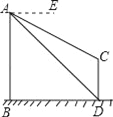
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
【答案】(1)两建筑物底部之间水平距离BD的长度为60米;
(2)建筑物CD的高度为(60﹣20![]() )米.
)米.
【解析】试题分析:
(1)由已知可判断△ABD是等腰直角三角形;
(2)过点A作DC延长线的垂线,垂足为点F,则在Rt△AFC,求出FC的长,再求CD的长.
试题解析:
(1)根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,
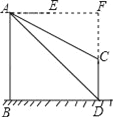
根据题意得四边形ABDF为正方形,
∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,
∴CF=AFtan∠FAC=60×![]() =20
=20![]() ,
,
又∵FD=60,
∴CD=60﹣20![]() ,
,
∴建筑物CD的高度为(60﹣20![]() )米.
)米.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】2017年元旦期间,某商场打出促销广告,如表所示.
优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元,但不超过500元 | 一次性购物超过500元 |
优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠,超过500元部分按八折优惠 |
小欣妈妈两次购物分别用了134元和490元.
(1)小欣妈妈这两次购物时,所购物品的原价分别为多少?
(2)若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.
