Question

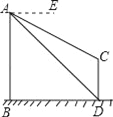
【题目】(9分)如图，已知DG⊥BC，AC⊥BC，EF⊥AB，∠1＝∠2.试说明CD⊥AB.

解：∵DG⊥BC，AC⊥BC(已知)，

∴∠DGB＝∠ACB＝90°(垂直定义).

∴DG∥AC(__________________).

∴∠2＝∠________(两直线平行，内错角相等).

∵∠1＝∠2(已知)，

∴∠1＝∠________(等量代换).

∴EF∥CD(__________________).

∴∠AEF＝∠________ (__________________).

∵EF⊥AB(已知)．

∴∠AEF＝90°(__________________).

∴∠ADC＝90°(__________________)．

∴CD⊥AB(__________________)．

Answer 1

【答案】解：同位角相等，两直线平行;ACD;ACD;同位角相等，两直线平行;ADC,两直线平行，同位角相等;垂直定义;等量代换;垂直定义.

【解析】试题分析：由DG⊥BC，AC⊥BC，则可得∠DGB=∠ACB=90°，根据平行线的判定定理可得DG∥AC；接下来根据平行线的性质可得：∠2=∠DCA，结合∠1=∠2可得到：∠1=∠DCA，继而推出CD∥EF；接下来根据EF⊥AB，CD∥EF，可得到CD与AB的位置关系.

解：∵DG⊥BC，AC⊥BC(已知)，

∴∠DGB＝∠ACB＝90°(垂直定义).

∴DG∥AC(同位角相等，两直线平行).

∴∠2＝∠ACD (两直线平行，内错角相等).

∵∠1＝∠2(已知)，

∴∠1＝∠ACD (等量代换).

∴EF∥CD(同位角相等，两直线平行).

∴∠AEF＝∠ADC, (两直线平行，同位角相等).

∵EF⊥AB(已知)．

∴∠AEF＝90°(垂直定义).

∴∠ADC＝90°(等量代换)．

∴CD⊥AB(垂直定义)．