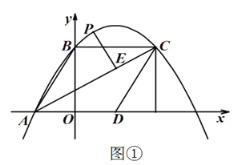
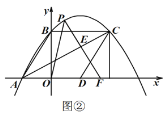
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§“―÷ΣΒψAΘ®0Θ§3mΘ©Θ§PΘ®0Θ§2mΘ©Θ§QΘ®0Θ§mΘ©(mΓΌ0)Θ°ΫΪΒψA»ΤΒψPΥ≥ ±’κ–ΐΉΣ90ΓψΘ§ΒΟΒΫΒψMΘ§ΫΪΒψO»ΤΒψQΥ≥ ±’κ–ΐΉΣ90ΓψΘ§ΒΟΒΫΒψNΘ§Ν§Ϋ”MNΘ§≥ΤœΏΕΈMNΈΣœΏΕΈAOΒΡΑιΥφœΏΕΈΘ°
Θ®1Θ©»γΆΦ1Θ§»τm=1Θ§‘ρΒψMΘ§NΒΡΉχ±ξΖ÷±πΈΣ Θ§ ΘΜ
Θ®2Θ©Ε‘”Ύ»Έ“βΒΡmΘ§«σΒψMΘ§NΒΡΉχ±ξΘ®”ΟΚ§mΒΡ ΫΉ”±μ ΨΘ©ΘΜ
Θ®3Θ©“―÷ΣΒψBΘ®![]() Θ§tΘ©Θ§CΘ®
Θ§tΘ©Θ§CΘ®![]() Θ§tΘ©Θ§“‘œΏΕΈBCΈΣ÷±ΨΕΘ§‘Ύ÷±œΏBCΒΡ…œΖΫΉςΑκ‘≤Θ§»τΑκ‘≤”κœΏΕΈBCΈß≥…ΒΡ«χ”ρΡΎΘ®Αϋά®±ΏΫγΘ©÷Ν…Ό¥φ‘Ύ“ΜΧθœΏΕΈAOΒΡΑιΥφœΏΕΈMNΘ§÷±Ϋ”–¥≥ωtΒΡ»Γ÷ΒΖΕΈßΘ°
Θ§tΘ©Θ§“‘œΏΕΈBCΈΣ÷±ΨΕΘ§‘Ύ÷±œΏBCΒΡ…œΖΫΉςΑκ‘≤Θ§»τΑκ‘≤”κœΏΕΈBCΈß≥…ΒΡ«χ”ρΡΎΘ®Αϋά®±ΏΫγΘ©÷Ν…Ό¥φ‘Ύ“ΜΧθœΏΕΈAOΒΡΑιΥφœΏΕΈMNΘ§÷±Ϋ”–¥≥ωtΒΡ»Γ÷ΒΖΕΈßΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©(1,2)Θ§(1,1) Θ°Θ®2Θ©(m,2 m)Θ§(m, m)Θ°Θ®3Θ©![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©Α―m=1Ζ÷±π¥ζ»κΒψAΘ§PΘ§QΒΡΉχ±ξ÷–Θ§“άΨίΧβ“βΫχ––≤ΌΉςΦ¥Ω…ΒΟΒΫMΘ§NΒΡΉχ±ξΘΜ
Θ®2Θ©ΗυΨίΒψAΘ§PΘ§QΒΡΉχ±ξ«σ≥ωAPΘ§OPΘ§OQΒΡ≥ΛΘ§‘ΌΗυΨί–ΐΉΣΒΡ–‘÷ Ω…«σ≥ωMΘ§NΒΡΉχ±ξΘΜ
Θ®3Θ©Ζ÷mΈΣ’ΐ ΐΚΆΗΚ ΐΝΫ÷÷«ιΩωΧ÷¬έ«σΫβΦ¥Ω….
Θ®1Θ©ΓΏAΘ®0Θ§3mΘ©Θ§PΘ®0Θ§2mΘ©Θ§QΘ®0Θ§mΘ©
ΓύΒ±m=1 ±Θ§AΘ®0Θ§3Θ©Θ§PΘ®0Θ§2Θ©Θ§QΘ®0Θ§1Θ©
ΓΏΒψA»ΤΒψPΥ≥ ±’κ–ΐΉΣ90ΓψΘ§ΒΟΒΫΒψMΘ§
ΓύMΘ®1Θ§2Θ©
ΓΏΒψO»ΤΒψQΥ≥ ±’κ–ΐΉΣ90ΓψΘ§ΒΟΒΫΒψNΘ§
ΓύN(-1,1)Θ§»γΆΦΥυ ΨΘΚ
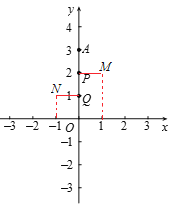
Θ®2Θ©ΓΏAΘ®0Θ§3mΘ©Θ§PΘ®0Θ§2mΘ©Θ§QΘ®0Θ§mΘ©
ΓύAP=mΘ§OP=2mΘ§OQ=m
ΓΏΒψA»ΤΒψPΥ≥ ±’κ–ΐΉΣ90ΓψΘ§ΒΟΒΫΒψMΘ§
ΓύMΘ®mΘ§2mΘ©
ΓΏΒψO»ΤΒψQΥ≥ ±’κ–ΐΉΣ90ΓψΘ§ΒΟΒΫΒψNΘ§
ΓύN(-mΘ§m)ΘΜ
Θ®3Θ©ΓΏΒψBΘ®![]() Θ§tΘ©Θ§CΘ®
Θ§tΘ©Θ§CΘ®![]() Θ§tΘ©Θ§
Θ§tΘ©Θ§
ΓύBC=2![]()
“‘œΏΕΈBCΈΣ÷±ΨΕΘ§‘Ύ÷±œΏBCΒΡ…œΖΫΉςΑκ‘≤Θ§»γΆΦΥυ ΨΘ§
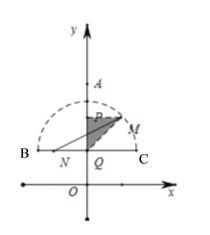
ΔΌΒ±mΈΣ’ΐ ΐ ±Θ§Ακ‘≤÷–œΏΕΈMNΒΡΉν¥σ÷Β «N‘ΎBC…œΘ§M‘ΎΜΓ…œΘ§
¥Υ ±ΓςPQM «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
Γύ![]() Θ§Φ¥
Θ§Φ¥![]()
ΫβΒΟm=1Μρm=-1(…α»Ξ)Θ§
ΓύQO=1Θ§
Γύt=1;
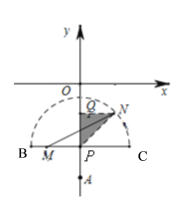
ΔΎΒ±mΈΣΗΚ ΐ ±Θ§Ακ‘≤÷–œΏΕΈMNΒΡΉν–Γ÷Β «M‘ΎBC…œΘ§N‘ΎΜΓ…œΘ§¥Υ ±ΓςPQM «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§»γΆΦΘ§
Γύ![]() Θ§Φ¥
Θ§Φ¥![]()
ΫβΒΟm=-1Μρm=1(…α»Ξ)Θ§
ΓύPO=2Θ§
Γύt=-2;
Ι ![]()

 ΦΤΥψΗΏ ÷œΒΝ–¥πΑΗ
ΦΤΥψΗΏ ÷œΒΝ–¥πΑΗΓΨΧβΡΩΓΩ≤Έ’’―ßœΑΚ· ΐΒΡΙΐ≥Χ”κΖΫΖ®Θ§ΧΫΨΩΚ· ΐy=![]() ΒΡΆΦœσ”κ–‘÷ Θ°
ΒΡΆΦœσ”κ–‘÷ Θ°
“ρΈΣy=![]() Θ§Φ¥y=©¹
Θ§Φ¥y=©¹![]() +1Θ§Υυ“‘Έ“Ο«Ε‘±»Κ· ΐy=©¹
+1Θ§Υυ“‘Έ“Ο«Ε‘±»Κ· ΐy=©¹![]() ά¥ΧΫΨΩΘ°
ά¥ΧΫΨΩΘ°
Ν–±μΘΚ
x | Γ≠ | ©¹4 | ©¹3 | ©¹2 | ©¹1 | ©¹ |
| 1 | 2 | 3 | 4 | Γ≠ |
y=©¹ | Γ≠ |
|
| 1 | 2 | 4 | ©¹4 | ©¹1 | 1 | ©¹ | ©¹ | Γ≠ |
y= | Γ≠ |
|
| 2 | 3 | 5 | ©¹3 | ©¹1 | 0 |
|
| Γ≠ |
ΟηΒψΘΚ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“‘Ή‘±δΝΩxΒΡ»Γ÷ΒΈΣΚαΉχ±ξΘ§“‘y=![]() œύ”ΠΒΡΚ· ΐ÷ΒΈΣΉίΉχ±ξΘ§Οη≥ωœύ”ΠΒΡΒψΘ§»γΆΦΥυ ΨΘΚ
œύ”ΠΒΡΚ· ΐ÷ΒΈΣΉίΉχ±ξΘ§Οη≥ωœύ”ΠΒΡΒψΘ§»γΆΦΥυ ΨΘΚ
Θ®1Θ©«κΑ―y÷αΉσ±ΏΗςΒψΚΆ”“±ΏΗςΒψΘ§Ζ÷±π”Ο“ΜΧθΙβΜ§«ζœΏΥ≥¥ΈΝ§Ϋ”Τπά¥ΘΜ
Θ®2Θ©Ιέ≤λΆΦœσ≤ΔΖ÷Έω±μΗώΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
ΔΌΒ±xΘΦ0 ±Θ§yΥφxΒΡ‘ω¥σΕχΓΓ ΓΓΘΜΘ®ΧνΓΑ‘ω¥σΓ±ΜρΓΑΦθ–ΓΓ±Θ©
ΔΎy=![]() ΒΡΆΦœσ «”…y=©¹
ΒΡΆΦœσ «”…y=©¹![]() ΒΡΆΦœσœρΓΓ ΓΓΤΫ“ΤΓΓ ΓΓΗωΒΞΈΜΕχΒΟΒΫΘΜ
ΒΡΆΦœσœρΓΓ ΓΓΤΫ“ΤΓΓ ΓΓΗωΒΞΈΜΕχΒΟΒΫΘΜ
ΔέΆΦœσΙΊ”ΎΒψΓΓ ΓΓ÷––ΡΕ‘≥ΤΘ°Θ®ΧνΒψΒΡΉχ±ξΘ©
Θ®3Θ©…ηAΘ®x1Θ§y1Θ©Θ§BΘ®x2Θ§y2Θ© «Κ· ΐy=![]() ΒΡΆΦœσ…œΒΡΝΫΒψΘ§«“x1+x2=0Θ§ ‘«σy1+y2+3ΒΡ÷ΒΘ°
ΒΡΆΦœσ…œΒΡΝΫΒψΘ§«“x1+x2=0Θ§ ‘«σy1+y2+3ΒΡ÷ΒΘ°
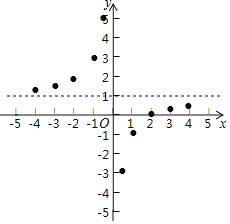
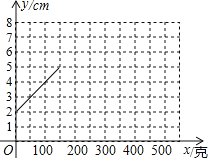
ΓΨΧβΡΩΓΩΒ·Μ… «“Μ÷÷άϊ”ΟΒ·–‘ά¥ΙΛΉςΒΡΜζ–ΒΝψΦΰΘ§”ΟΒ·–‘≤ΡΝœ÷Τ≥…ΒΡΝψΦΰ‘ΎΆβΝΠΉς”Οœ¬ΖΔ…ζ–Έ±δΘ§≥ΐ»ΞΆβΝΠΚσ”÷Μ÷Η¥‘≠Ή¥Θ°Ρ≥ΑύΆ§―ß‘ΎΧΫΨΩΒ·Μ…ΒΡ≥ΛΕ»”κΥυ ήΆβΝΠΒΡ±δΜ·ΙΊœΒ ±Θ§Ά®Ιΐ Β―ιΦ«¬ΦΒΟΒΫΒΡ ΐΨί»γœ¬±μΘΚ
μά¬κΒΡ÷ ΝΩxΘ®ΩΥΘ© | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
÷Η’κΒΡΈΜ÷ΟyΘ®cmΘ© | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
–ΓΧΎΗυΨί―ßœΑΚ· ΐΒΡΨ≠―ιΘ§άϊ”Ο…œ ω±μΗώΥυΖ¥”≥≥ωΒΡy”κx÷°ΦδΒΡ±δΜ·Ιφ¬…Θ§Ε‘ΗΟΚ· ΐΒΡΆΦœσ”κ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ§œ¬Οφ «–ΓΧΎΒΡΧΫΨΩΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘ°
Θ®1Θ©ΗυΨί…œ ω±μΗώ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–≤Ι»ΪΗΟΚ· ΐΒΡΆΦœσΘΜ
Θ®2Θ©ΗυΨίΜ≠≥ωΒΡΚ· ΐΆΦœσΘ§–¥≥ωΘΚ
ΔΌΒ±xΘΫ0 ±Θ§yΘΫΓΓ ΓΓΘ§ΥϋΒΡ ΒΦ “β“ε «ΓΓ ΓΓΘΜ
ΔΎΒ±÷Η’κΒΡΈΜ÷Οy≤Μ±δ ±Θ§μά¬κΒΡ÷ ΝΩxΒΡ»Γ÷ΒΖΕΈßΈΣΓΓ ΓΓΘ°
ΓΨΧβΡΩΓΩ“―÷ΣΙΊ”Ύ![]() ΒΡΕΰ¥ΈΚ· ΐ
ΒΡΕΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσΩΣΩΎœρœ¬Θ§
ΒΡΆΦœσΩΣΩΎœρœ¬Θ§![]() ”κ
”κ![]() ΒΡ≤ΩΖ÷Ε‘”Π÷Β»γœ¬±μΥυ ΨΘΚ
ΒΡ≤ΩΖ÷Ε‘”Π÷Β»γœ¬±μΥυ ΨΘΚ
|
|
|
|
|
|
|
|
|
|
|
|
œ¬Ν–≈–ΕœΘ§ΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() ΘΜΔέΖΫ≥Χ
ΘΜΔέΖΫ≥Χ![]() ”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘΜ
”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘΜ
Δή»τ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§’ΐ»ΖΒΡ «________________(Χν–¥’ΐ»Ζ¥πΑΗΒΡ–ρΚ≈) Θ°
Θ§’ΐ»ΖΒΡ «________________(Χν–¥’ΐ»Ζ¥πΑΗΒΡ–ρΚ≈) Θ°