题目内容
【题目】如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.

(1)求证:BD=BE;
(2)若DBC=30,CD=4,求四边形ABED的面积.
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】
试题分析:(1)先根据两组对边分别平行证明四边形ABEC 是平行四边形,再根据平行四边形的性质和矩形的性质可以证得BD=BE.(2) 四边形ABED是梯形,本题关键是求出高BC,再根据梯形面积公式求出答案为![]() .
.
试题解析:(1)证明:∵四边形ABCD是矩形,∴AC=BD,AB∥CD ,又BE ∥AC , ∴四边形ABEC 是平行四边形 ,∴BE= AC ,∴BD=BE ,(2)∵四边形ABCD是矩形 , 四边形ABEC 是平行四边形,∴AB=DC=CE=4,在Rt △DBC 中,∠DBC=30°,![]() ,即
,即![]() ,解得
,解得![]() ,∵AB∥DE ,AD与BE不平行,∴四边形ABED是梯形,且BC为梯形的高,
,∵AB∥DE ,AD与BE不平行,∴四边形ABED是梯形,且BC为梯形的高,
∴四边形ABED的面积![]() .
.
考点:①解直角三角形;②平行四边形的性质;③矩形的性质与判定.

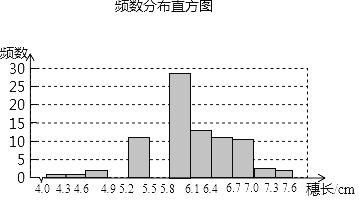
【题目】为了考察某种大麦细长的分布情况,在一块试验田里抽取了部分麦穗.测得它们的长度,数据整理后的频数分布表及频数分直方图如下.根据以下信息,解答下列问题:
穗长x | 频数 |
4.0≤x<4.3 | 1 |
4.3≤x<4.6 | 1 |
4.6≤x<4.9 | 2 |
4.9≤x<5.2 | 5 |
5.2≤x<5.5 | 11 |
5.5≤x<5.8 | 15 |
5.8≤x<6.1 | 28 |
6.1≤x<6.4 | 13 |
6.4≤x<6.7 | 11 |
6.7≤x<7.0 | 10 |
7.0≤x<7.3 | 2 |
7.3≤x<7.6 | 1 |
(Ⅰ)补全直方图;
(Ⅱ)共抽取了麦穗 棵;
(Ⅲ)频数分布表的组距是 ,组数是 ;
(Ⅳ)麦穗长度在5.8≤x<6.1范围内麦穗有多少棵?占抽取麦穗的百分之几?