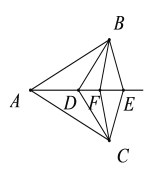题目内容
【题目】如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( )

A. 1对 B. 2对 C. 3对 D. 4对
【答案】D
【解析】
根据点D,E,F分别为OA,OB,OC的中点,可得DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,可得DE//AB,DF//AC,EF//BC,进而可判定△DOE∽△AOD, △DOF∽△AOC, △EOF∽△BOC,根据中位线性质可得![]() ,
,![]() ,
,
继而可得![]() ,可判定△DEF∽△ABC.
,可判定△DEF∽△ABC.
因为点D,E,F分别为OA,OB,OC的中点,
所以DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,
所以DE//AB,DF//AC,EF//BC,
所以△DOE∽△AOD, △DOF∽△AOC, △EOF∽△BOC,
因为DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,
所以![]() ,
,![]() ,
,
所以![]() ,
,
所以△DEF∽△ABC,
因此有四对相似三角形,
故选D.

练习册系列答案
相关题目