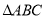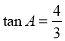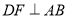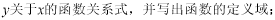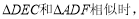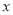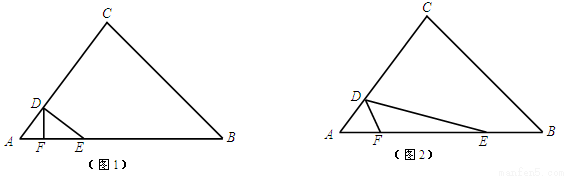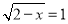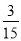Question

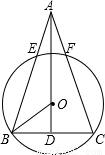
如图，已知在△ABC中，AB=AC，BC=8，tan∠ABC=3，AD⊥BC于D，O是AD上一点，OD=3，以OB为半径的⊙O分别交AB、AC于E、F．求：

（1）⊙O的半径；

（2）BE的长．

 

 

Answer 1

(1)5;(2) ．

【解析】

试题分析：（1）根据等腰三角形性质求出BD，根据勾股定理求出OB即可；

（2）根据垂径定理得出BH=HE，证三角形AHO和三角形ADB相似，得出比例式，求出AH，求出AB，求出BH即可．

试题解析：（1）∵AB=AC，AD⊥BC，BC=8，

∴BD=CD=4，

在RT△BOD中∵OD=3，

∴由勾股定理得：OB=5；

（2）过O点作OH⊥AB，交AB于H，

又∵OH过圆心O，

∴BH=EH，

∵在RT△ABD中，tan∠ABD=，

∴AD=12，由勾股定理得：AB=4，

∵OD=3，

∴AO=9，

∵∠OAH=∠BAD，∠OHA=∠ADB，

∵△AOH∽△ABD，

∴，

∴，

∴AH=，

∴BH=，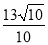

∴BE=．

考点：1.相似三角形的判定与性质；2.等腰三角形的性质；3.垂径定理；4.解直角三角形．