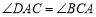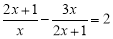题目内容
在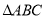 中,AC=25,AB=35,
中,AC=25,AB=35,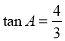 ,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
(1)如图1,当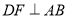 时,求AE的长;
时,求AE的长;
(2)如图2,当点E、F在边AB上时,求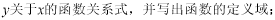
(3)联结CE,当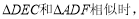 求
求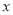 的值.
的值.
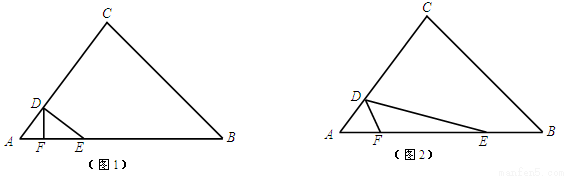
(1)AE=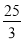 ;(2)
;(2)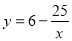 (
( );(3)当△DEC和△ADF相似时
);(3)当△DEC和△ADF相似时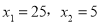 ,
,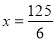
【解析】
试题分析:
(1)先根据DF⊥AB,∠EDF=∠A,得出∠ADE=90°,再根据AD=5,tanA=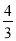 ,即可求出AE;
,即可求出AE;
(2)过点D作DG⊥AB,交AB于G,先证出△EDF∽△EAD,得出ED2=AE•EF,再求出DG、AG,最后根据EG=x-6,DE2=42+(x-3)2得出42+(x-3)2=x•(x-y),再进行整理即可;
(3)先证出∠AFD=∠EDC,再分两种情况讨论:①当∠A=∠CED时,得出AD:AC=AF:AE,5:25=y:x,再把y=6-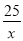 代入得出5(6-
代入得出5(6-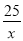 )=x,再解方程即可;
)=x,再解方程即可;
②当∠A=∠DCE时,根据△ECD∽△DAF得出CD:AF=CE:AD,20:y=x:5,再把y=6-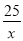 代入得出5(6-
代入得出5(6-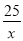 )=x,求出方程的解即可.
)=x,求出方程的解即可.
试题解析:
∵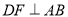 ,
,
∴ ,
,
∴
∵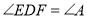 ,
,
∴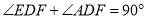 ,即
,即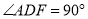
在 ,
,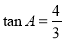
∴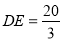
∴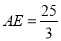
(2)过点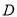 作
作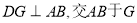
∵ ,
,
∴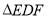 ∽
∽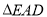
∴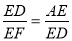
∴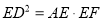
∴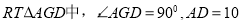

∴ ∴
∴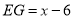 ∴
∴
∴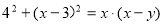
∴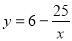 (
(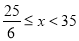 )
)
(3)∵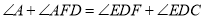 ,且
,且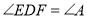 .
.
∴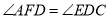
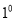 当
当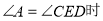
∵ ,又∵
,又∵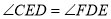 ∴
∴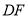 //
//
∴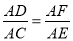 ∴
∴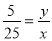 ∵
∵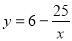 ∴
∴
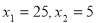
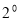 当
当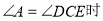
∵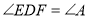 ,∴
,∴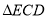 ∽
∽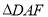
∴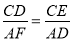
∴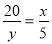
∵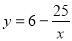
∴
∴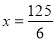
综上当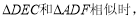
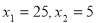 ,
,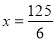 .
.
考点:相似形综合题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目