题目内容
【题目】已知等边△ABC中,在射线BA上有一点D,连接CD,并以CD为边向上作等边△CDE,连接BE和AE.试判断下列结论:①AE=BD; ②AE与AB所夹锐夹角为60°;③当D在线段AB或BA延长线上时,总有∠BDE-∠AED=2∠BDC;④∠BCD=90°时,CE2+AD2=AC2+DE2 .正确的序号有( )

A. ①② B. ①②③ C. ①②④ D. ①②③④
【答案】C
【解析】
由∠BCD=∠ACD+60°,∠ACE=∠ACD+60°可得∠BCD=∠ACE,利用SAS可证明△BCD≌△ACE,可得AE=BD,①正确;∠CBD=∠CAE=60°,进而可得∠EAD=60°,②正确,当∠BCD=90°时,可得∠ACD=∠ADC=30°,可得AD=AC,即可得CE2+AD2=AC2+DE2 ,④正确;当D点在BA延长线上时,∠BDE-∠BDC=60°,根据△BCD≌△ACE可得∠AEC=∠BDC,进而可得∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,即可证明∠BDE-∠BDC=∠BDC+∠AED,即∠BDE-∠AED=2∠BDC,当点D在AB上时可证明∠BDE-∠AED=120°,③错误,综上即可得答案.
∵∠BCA=∠DCE=60°,
∴∠BCA+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
又∵AC=BC,CE=CD,
∴△BCD≌△ACE,
∴AE=BD,∠CBA=∠CAE=60°,∠AEC=∠BDC,①正确,
∴∠BAE=120°,
∴∠EAD=60°,②正确,
∵∠BCD=90°,∠BCA=60°,
∴∠ACD=∠ADC=30°,
∴AC=AD,
∵CE=DE,
∴CE2+AD2=AC2+DE2,④正确,
当D点在BA延长线上时,∠BDE-∠BDC=60°,
∵∠AEC=∠BDC,
∴∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,
∴∠BDE-∠BDC=∠BDC+∠AED
∴∠BDE-∠AED=2∠BDC,

如图,当点D在AB上时,
∵△BCD≌△∠ACE,
∴∠CAE=∠CBD=60°,
∴∠DAE=∠BAC+∠CAE=120°,
∴∠BDE-∠AED=∠DAE=120°,③错误
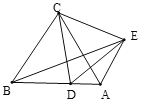
故正确的结论有①②④,
故选C.