题目内容
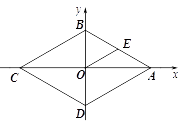
【题目】如图1,将正方形 ![]() 置于平面直角坐标系中,其中
置于平面直角坐标系中,其中 ![]() 边在
边在 ![]() 轴上,其余各边均与坐标轴平行.直线
轴上,其余各边均与坐标轴平行.直线 ![]() 沿
沿 ![]() 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形
轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形 ![]() 的边所截得的线段长为
的边所截得的线段长为 ![]() ,平移的时间为
,平移的时间为 ![]() (秒),
(秒), ![]() 与
与 ![]() 的函数图象如图2所示,则图1中的点
的函数图象如图2所示,则图1中的点 ![]() 的坐标为 , 图2中
的坐标为 , 图2中 ![]() 的值为.
的值为.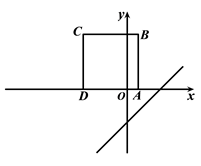

图1 图2
【答案】(1,0);5 ![]()
【解析】解:令直线y=x-3=0,解得x=3,即可得直线y=x-3与x轴的交点坐标为(3,0),根据图 2 可知,开始平移2s后直线到达点A,所以点A横坐标为3-2=1,所以点A坐标为(1,0);由图象2可知,直线y=x-3平移12s时,正好经过点C,此时平移后的直线与x轴交点的横坐标为(-9,0),所以点A到这个交点的距离为10,即可得AD=5,根据勾股定理求得BD=5 ![]() ,当y=x-3平移到BD的位置时m最大,即m最大为5
,当y=x-3平移到BD的位置时m最大,即m最大为5 ![]() ,所以b=5
,所以b=5 ![]() .
.
【考点精析】利用勾股定理的概念对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目