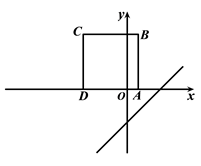题目内容
【题目】如图,在方格纸中,三角形ABC的三个顶点和点P都在小方格的顶点上.
(1)请在图1中,画出将三角形ABC绕点C旋转后的三角形A1B1C,使得点P落在三角形A1B1C内部,且三角形A1B1C的顶点也都落在方格的顶点上.
(2)写出旋转角的度数 .
(3)拓展延伸:如图2,将直角三角形ABC(其中∠C=90°)绕点A按顺时针方向选择115°得到△AB1C1 , 使得点C,A,B1在同一条直线上,那么∠BAC1等于 .
【答案】
(1)解:如图所示: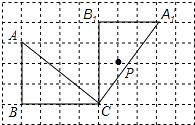
(2)90°
(3)50°
【解析】解:(2)旋转角的度数为90°;(3)∵点C,A,B1在同一条直线上,
∴∠CAB1=180°,
∵绕点A按顺时针方向选择115°,
∴∠BAC=180°﹣115°=65°,
根据旋转可得∠BAC=∠C1AB1=65°,
∴∠BAC1=180°﹣65°﹣65°=50°,
故答案为:50°.
(1)旋转的性质: ①对应点到旋转中心的距离相等(旋转中心在对应点所连线段的垂直平分线上)。②对应点与旋转中心所连线段的夹角等于旋转角。 ③旋转前、后的图形全等。根据性质画出图形;(2)由题意可知旋转角的度数为90°;(3)根据点C,A,B1在同一条直线上,可得∠CAB1=180°,根据旋转的性质可得∠BAC=∠C1AB1=65°,∠BAC1的度数可求。

练习册系列答案
相关题目