Question

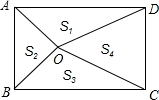
在矩形ABCD中，AB=2，AD=3，∠DAB和∠ABC的平分线交于点O，连结OC，OD，将矩形分成四等分，四部分的面积分别记为S₁，S₂，S₃，S₄，如图所示，则S₁：S₂：S₃：S₄等于（　　）

A．3：2：3：2

B．3：2：2：4

C．3：2：3：3

D．3：2：3：4

Answer 1

在矩形ABCD中，∠DAB=∠ABC=90°，
∵∠DAB和∠ABC的平分线交于点O，
∴∠OAB=∠OBA=

1

2

×90°=45°，
∴△AOB是等腰直角三角形，
∴点O到AB、BC、AD的距离都是：

1

2

AB=

1

2

×2=1，
∵CD=3，
∴点O到CD的距离是3-1=2，
∴S₁=

1

2

×3×1=1.5，S₂=

1

2

×2×1=1，S₃=

1

2

×3×1=1.5，S₄=

1

2

×2×2=2，
∴S₁：S₂：S₃：S₄=1.5：1：1.5：2=3：2：3：4．
故选D．