题目内容
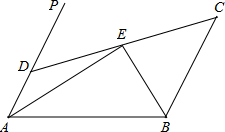 如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.
如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.分析:首先在AB上截取AF=AD,由AE平分∠PAB,利用SAS即可证得△DAE≌△FAE,继而可证得∠EFB=∠C,然后利用AAS证得△BEF≌△BEC,即可得BC=BF,继而证得AD+BC=AB.
解答: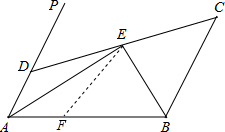 证明:在AB上截取AF=AD,
证明:在AB上截取AF=AD,
∵AE平分∠PAB,
∴∠DAE=∠FAE,
在△DAE和△FAE中,
∵
,
∴△DAE≌△FAE(SAS),
∴∠AFE=∠ADE,
∵AD∥BC,
∴∠ADE+∠C=180°,
∵∠AFE+∠EFB=180°,
∴∠EFB=∠C,
∵BE平分∠ABC,
∴∠EBF=∠EBC,
在△BEF和△BEC中,
∵
,
∴△BEF≌△BEC(AAS),
∴BC=BF,
∴AD+BC=AF+BF=AB.
 证明:在AB上截取AF=AD,
证明:在AB上截取AF=AD,∵AE平分∠PAB,
∴∠DAE=∠FAE,
在△DAE和△FAE中,
∵
|
∴△DAE≌△FAE(SAS),
∴∠AFE=∠ADE,
∵AD∥BC,
∴∠ADE+∠C=180°,
∵∠AFE+∠EFB=180°,
∴∠EFB=∠C,
∵BE平分∠ABC,
∴∠EBF=∠EBC,
在△BEF和△BEC中,
∵
|
∴△BEF≌△BEC(AAS),
∴BC=BF,
∴AD+BC=AF+BF=AB.
点评:此题考查了全等三角形的判定与性质以及平行线的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 9、如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC=
9、如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC=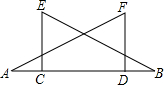 如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是
如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是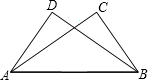 如图,已知AD=BC,AC=BD,∠DAC与∠CBD有什么关系?说说你的理由.
如图,已知AD=BC,AC=BD,∠DAC与∠CBD有什么关系?说说你的理由.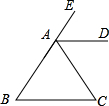 如图,已知AD∥BC,AD平分∠CAE,试说明△ABC是等腰三角形.
如图,已知AD∥BC,AD平分∠CAE,试说明△ABC是等腰三角形.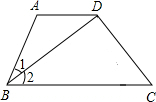 如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠C=
如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠C=