题目内容
如图，已知AD∥BC，∠1=∠2，∠A=112°，且BD⊥CD，则∠C=56°
56°
．分析：根据平行线的性质，得∠2=∠ADB，从而根据三角形的内角和定理，即可求得∠1、∠2的度数．再根据直角三角形的两个锐角互余求得∠C的度数．
解答：解：∵AD∥BC，
∴∠2=∠ADB．
又∵∠1=∠2，∠A=112°，
∴∠1=∠2=∠ADB=34°．
∴∠C=90°-34°=56°，
故答案为：56°．
∴∠2=∠ADB．
又∵∠1=∠2，∠A=112°，
∴∠1=∠2=∠ADB=34°．
∴∠C=90°-34°=56°，
故答案为：56°．
点评：此题综合运用了三角形的内角和定理、平行线的性质．三角形的内角和是180°；两条直线平行，则同位角相等，内错角相等，同旁内角互补．
练习册系列答案
相关题目
9、如图，已知AD∥BC，∠1=∠2，∠A=112°，且BD⊥CD，则∠ABC=
如图，已知AD=BC．EC⊥AB．DF⊥AB，C．D为垂足，要使△AFD≌△BEC，还需添加一个条件．若以“ASA”为依据，则添加的条件是
如图，已知AD=BC，AC=BD，∠DAC与∠CBD有什么关系？说说你的理由．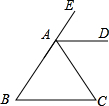
如图，已知AD∥BC，AD平分∠CAE，试说明△ABC是等腰三角形．