题目内容
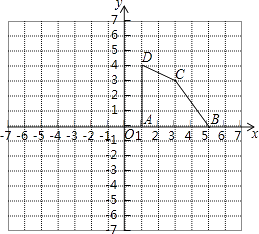
【题目】如图,若AD∥BC,∠A=∠D. 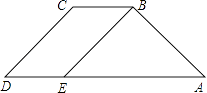
(1)猜想∠C与∠ABC的数量关系,并说明理由;
(2)若CD∥BE,∠D=50°,求∠EBC的度数.
【答案】
(1)解:∵AD∥BC,
∴∠D+∠C=180°,∠A+∠ABC=180°,
∵∠A=∠D,
∴∠C=∠ABC;
(2)解:∵CD∥BE,
∴∠D=∠AEB.
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠D=∠EBC=50°.
【解析】(1)先根据平行线的性质得出∠D+∠C=180°,∠A+∠ABC=180°,再根据∠A=∠D即可得出结论;(2)根据CD∥BE可得出∠D=∠AEB,再由AD∥BC即可得出结论.
【考点精析】通过灵活运用平行线的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.

练习册系列答案
相关题目
【题目】九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
(1)把下面的频数分布表和频数分布直方图补充完整;
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | 0.24 | |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | |
25<x≤30 | 2 | 0.04 |
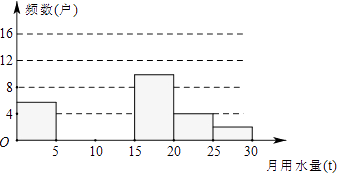
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?