题目内容
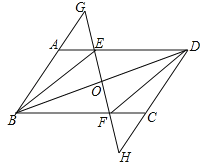
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点0.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什幺特殊四边形?请说明理由.
【答案】(1)证明见解析;(2)四边形BEDF是菱形.
【解析】
试题分析:(1)由平行四边形的性质得出AB=CD,∠BAE=∠DCF,由SAS证明△ABE≌△CDF即可;
(2)由平行四边形的性质得出AD∥BC,AD=BC,证出DE=BF,得出四边形BEDF是平行四边形,得出OB=OD,再由等腰三角形的三线合一性质得出EF⊥BD,即可得出四边形BEDF是菱形.
试题解析:(1)∵四边形ABCD是平行四边形,∴AB=CD,∠BAE=∠DCF,在△ABE和△CDF中,∵AB=CD,∠BAE=∠DCF,AE=CF,∴△ABE≌△CDF(SAS);
(2)四边形BEDF是菱形;理由如下:如图所示:
∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵AE=CF,∴DE=BF,∴四边形BEDF是平行四边形,∴OB=OD,∵DG=BG,∴EF⊥BD,∴四边形BEDF是菱形.

练习册系列答案
相关题目