题目内容
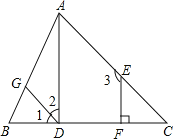
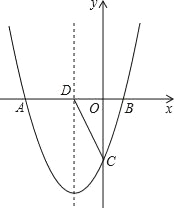
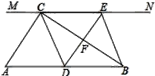
【题目】如图,在 Rt △ ABC 中,∠ ACB = 90 °,过点 C 的直线 MN ∥ AB , D 为 AB 边上一点,过点 D 作 DE ⊥ BC ,交直线 MN 于 E ,垂足为 F ,连接 CD 、 BE .(1)求证: CE = AD ;(2)当 D 在 AB 中点时,四边形 BECD 是什么特殊四边形?说明你的理由.
【答案】(1)见解析;(2)四边形 BECD 是菱形,理由见解析.
【解析】
(1)利用平行四边形对边平行可解答.
(2)利用证明菱形的条件即可解答.
证明:∵ DE ⊥ BC ,
∴∠ DFB = 90 °,
∵∠ ACB = 90 °,
∴∠ ACB =∠ DFB ,
∴ AC ∥ DE ,
∵ MN ∥ A B ,即 CE ∥ AD ,
∴四边形 ADEC 是平行四边形,
∴ CE = AD ;
( 2 )解:四边形 BECD 是菱形,理由如下:
∵ D 为 AB 中点,
∴ AD = BD ,
∵ CE = AD ,
∴ BD = CE ,
∵ BD ∥ CE ,
∴四边形 BECD 是平行四边形,
∵∠ ACB = 90 °, D 为 AB 中点,
∴ CD = BD ,
∴四边形 BECD 是菱形.

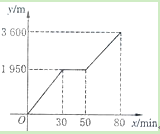
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
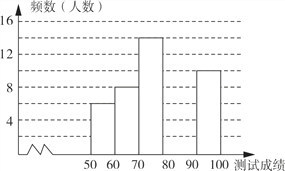
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
【题目】随着出行方式的多样化,某地区打车有三种乘车方式,收费标准如下(假设打车的平均车速为30千米/小时):
网约出租车 | 网约顺风车 | 网约专车 |
3千米以内:12元 | 1.5元/千米 | 2元/千米 |
超过3千米的部分:2.4元/千米 | 0.5元/分钟 | 0.6元/分钟 |
(如:乘坐6千米,耗时12分钟,网约出租车的收费为:12+2.4×(6-3)=19.2(元);网约顺风车的收费为:6×1.5+12×0.5=15(元);网约专车的收费为:6×2+12×0.6=19.2(元))
请据此信息解决如下问题:
(1)王老师乘车从纵棹园去汽车站,全程8千米,如果王老师乘坐网约出租车,需要支付的打车费用为______元;
(2)李校长乘车从纵掉园去生态园,乘坐网约顺风车比乘坐网约出租车节省了2元.求从纵棹园去生态园的路程;
(3)网约专车为了和网约顺风车竞争客户,分别推出了优惠方式:网约顺风车对于乘车路程在5千米以上(含5千米)的客户每次收费立减6元;网约专车打车车费一律七五折优惠.对采用哪一种打车方式更合算提出你的建议.