题目内容
我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离;即![]() ,也就是说,|x|表示在数轴上数x与数0对应点之间的距离;
,也就是说,|x|表示在数轴上数x与数0对应点之间的距离;
这个结论可以推广为![]() 表示在数轴上
表示在数轴上![]() ,
,![]() 对应点之间的距离;
对应点之间的距离;
例1:解方程![]() ,容易看出,在数轴下与原点距离为2点的对应数为±2,即该方程的解为x=±2
,容易看出,在数轴下与原点距离为2点的对应数为±2,即该方程的解为x=±2
例2:解不等式▏x-1▏>2,如图,在数轴上找出▏x-1▏=2的解,即到1的距离为2的点对应的数为-1、3,则▏x-1▏>2的解为x<-1或x>3
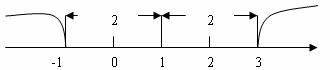
例3:解方程![]() 。由绝对值的几何意义知,该方程表示求在数轴上与1
。由绝对值的几何意义知,该方程表示求在数轴上与1
和-2的距离之和为5的点对应的x的值。在数轴上,1和-2的距离为3,满足方程的x对应点在1的右边或-2的左边,若x对应点在1的右边,由图可以看出x=2;同理,若x对应点在-2的左边,可得x=-3,故原方程的解是x=2或x=-3
参考阅读材料,解答下列问题:
(1)方程![]() 的解为
的解为
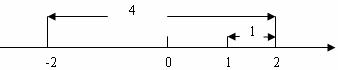
(2)解不等式![]() ≥9;
≥9;
(3)若![]() ≤a对任意的x都成立,求a的取值范围.
≤a对任意的x都成立,求a的取值范围.
解:(1)1或![]() .
.
(2)![]() 和
和![]() 的距离为7,
的距离为7,
因此,满足不等式的解对应的点3与![]() 的两侧.
的两侧.
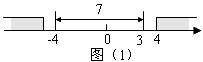
当![]() 在3的右边时,如图(1),
在3的右边时,如图(1),
易知![]() .
.
当![]() 在
在![]() 的左边时,如图(1),
的左边时,如图(1),
易知![]() .
.
![]() 原不等式的解为
原不等式的解为![]() 或
或![]()
(3)原问题转化为: ![]() 大于或等于
大于或等于![]() 最大值.
最大值.
当![]() 时,
时,![]() ,
,
当![]() ,
,![]() 随
随![]() 的增大而减小,
的增大而减小,
当![]() 时,
时,![]() ,
,
即![]() 的最大值为7.
的最大值为7.
故![]() .
.

练习册系列答案
相关题目
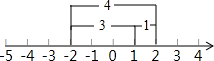 x的对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.根据上面的阅读材料,解答下列问题:
x的对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.根据上面的阅读材料,解答下列问题: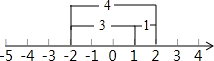 x的对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.根据上面的阅读材料,解答下列问题:
x的对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.根据上面的阅读材料,解答下列问题: