题目内容
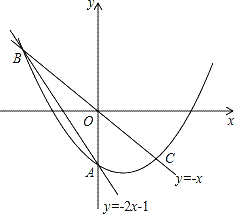
【题目】如图,在平面直角坐标系中,O为原点,直线y=2x﹣1,与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.
(1)求过A,B,C三点的抛物线的解析式;
(2)P为抛物线上一点,它关于原点的对称点为Q,当四边形PBQC为菱形时,求点P的坐标.
【答案】(1)抛物线解析式为y=x2-x-1;(2)P点坐标为(1-![]() ,1-
,1-![]() )或(1+
)或(1+![]() ,1+
,1+![]() ).
).
【解析】试题分析:本题主要考查二次函数的应用。
(1)由两直线解析式求出B点坐标,由题意B、C关于原点对称求出C坐标,再由y=2x-1与y轴交于点A,求出点A的坐标,即可用待定系数法确定二次函数解析式。
(2)①先由点P在抛物线上,设出点P的坐标。根据菱形的性质可知对角线垂直,则可得PQ所在直线的解析式,把点P代入该直线解析式可得点P的坐标。
解:(1)联立两直线解析式可得![]() ,解得
,解得![]() ,
,
∴B点坐标为(-1,1),
又C点为B点关于原点的对称点,
∴C点坐标为(1,-1),
∵直线y=-2x-1与y轴交于点A,
∴A点坐标为(0,-1),
设抛物线解析式为y=ax2+bx+c,
把A、B、C三点坐标代入可得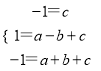 ,解得
,解得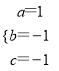 ,
,
∴抛物线解析式为y=x2-x-1;
(2)当四边形PBQC为菱形时,则PQ⊥BC,
∵直线BC解析式为y=-x,
∴直线PQ解析式为y=x,
联立抛物线解析式可得![]() ,解得
,解得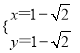 或
或 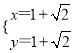 ,
,
∴P点坐标为(1-![]() ,1-
,1-![]() )或(1+
)或(1+![]() ,1+
,1+![]() ).
).

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).