题目内容
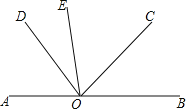
【题目】如图,已知,A、O、B在同一条直线上,∠AOE=∠COD,∠EOD=30°.
(1)若∠AOE=88°30′,求∠BOC的度数;
(2)若射线OC平分∠EOB,求∠BOC的度数.
【答案】(1) 33°;(2) ∠BOC=50°
【解析】
(1)先求出∠AOC度数,再利用∠AOC与∠BOC互补关系求解;
(2)由∠AOE=∠COD,易得∠AOD=∠COE,再借助角平分线定义分析出∠AOD=∠COE=∠BOC,根据这三个等角加上∠DOE等于180°列方程,从而可求出∠BOC度数.
(1)∵∠AOC=∠AOE+∠DOC-∠DOE =88°30′+88°30′-30°=147°,
∴∠BOC=180°-∠AOC =180°-147°=33°;
(2)∵∠AOE=∠COD,
∴∠AOE-∠DOE=∠COD-∠DOE,
即∠AOD=∠COE,
∵OC平分∠BOE,
∴∠BOC=∠COE,
∴∠BOC=∠COE=∠AOD,
设∠BOC=∠COE=∠AOD=x°,
则3x+30°=180°,解得x=50°,
所以∠BOC=50°.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
【题目】一次期中考试中A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:
A | B | C | D | E | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
【1】求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
【2】为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是标准分=(个人成绩-平均成绩)÷成绩标准差. 从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好.