题目内容
如图1,矩形ABCD中,AB=21,AD=12,E是CD边上的一点,CE=5,M是BC边上的中点,动点P从点A出发,沿AB边以每秒1个单位长度的速度向终点B运动,连结PM.设动点P的运动时间是t秒.

(1)求线段AE的长;
(2)当△ADE与△PBM相似时,求t的值;
(3)如图2,连接EP,过点P作PH⊥AE于H.①当EP平分四边形PMEH的面积时,求t的值;②以PE为对称轴作线段BC的轴对称图形B′C′,当线段B′C′与线段AE有公共点时,写出t的取值范围(直接写出答案).

(1)求线段AE的长;
(2)当△ADE与△PBM相似时,求t的值;
(3)如图2,连接EP,过点P作PH⊥AE于H.①当EP平分四边形PMEH的面积时,求t的值;②以PE为对称轴作线段BC的轴对称图形B′C′,当线段B′C′与线段AE有公共点时,写出t的取值范围(直接写出答案).
(1)AE=20;(2)t=13或t=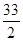 ;(3)①t=
;(3)①t=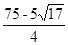 ②
②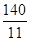 ≤t≤20.
≤t≤20.
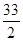 ;(3)①t=
;(3)①t=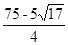 ②
②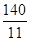 ≤t≤20.
≤t≤20.试题分析:(1)在直角三角形ADE中,已知AD=12,DE=16,根据勾股定理可求出AE的值;(2)分两种情况讨论:一、当∠DAE=∠PMB时,根据相似三角形的性质:相似三角形的对应边的比相等.即可求出t的值;二、当∠DAE=∠MPB时,由相似三角形的性质即可求出t的值.(3)①根据题意得出S△EHP=S△EMP,求出t的两个值,再根据t的取值范围即可求出t的值;②根据PE为对称轴作线段BC的轴对称图形B′C′,当点B′在线段AE上时,如图3所示,由勾股定理求得EB′=13,AB′=7,根据题意可证得△AB′N与△ADE相似,根据相似三角形对应边的比相等,可求出AN=5.6,NB′=4.2,则PN=t-5.6,PB′=21-t,再根据勾股定理可求出t的值为
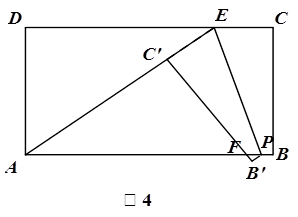
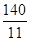 .当点C′在线段AE上时,如图4,则AC′=20-5=15,可证△AC′F与△ADE相似,可分别求出AF,C′F的值,在△PFB′中,利用勾股定理可求PF的值,从而求出AP的值,即求出t的值,所以有
.当点C′在线段AE上时,如图4,则AC′=20-5=15,可证△AC′F与△ADE相似,可分别求出AF,C′F的值,在△PFB′中,利用勾股定理可求PF的值,从而求出AP的值,即求出t的值,所以有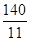 ≤t≤20.
≤t≤20.
试题解析:(1)∵ABCD是矩形,∴∠D=90°,∴AE2=AD2+DE2,∵AD=12,DE=16,∴AE=20;
(2)∵∠D=∠B=90°,∴△ADE与△PBM相似时,有两种可能;
当∠DAE=∠PMB时,有
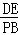 =
=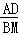 ,即
,即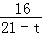 =
=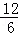 ,解得:t=13;
,解得:t=13;当∠DAE=∠MPB时,有
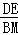 =
=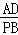 ,即
,即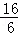 =
=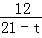 ,解得t=
,解得t=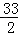 ;
;(3)①由题意得:S△EHP=S△EMP,
∴
 ×
×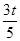 ×(20﹣
×(20﹣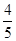 t)=
t)= ×12×(5+21﹣t)﹣
×12×(5+21﹣t)﹣ ×6×(21﹣t)﹣
×6×(21﹣t)﹣ ×6×5,
×6×5,解得:t=
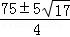 ,
,∵0<t<21,
∴t=
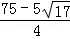 ;
;②根据题意得:
 ≤t≤20.
≤t≤20.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 x+2与两坐标轴交于A、B两点,将x轴沿AB翻折交双曲线y=
x+2与两坐标轴交于A、B两点,将x轴沿AB翻折交双曲线y= (x<0)于点C,若BC⊥AB,则k= .
(x<0)于点C,若BC⊥AB,则k= .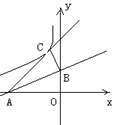





 在横杆
在横杆 的正上方,
的正上方, ,
, ,
, ,点
,点 的距离是3m,则点
的距离是3m,则点
 m
m


