题目内容
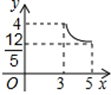
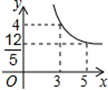
如图所示，在梯形ABCD中，AB∥DC，EF是梯形的中位线，AC交EF于G，BD交EF于H，以下说法错误的是（ ）.
| A．AB∥EF |
| B．AB+DC=2EF |
| C．四边形AEFB和四边形ABCD相似. |
| D．EG=FH |
C.
试题分析：根据梯形的中位线的性质进行解答.
在梯形ABCD中，AB∥DC，EF是梯形的中位线，所以AB∥EF，故A正确；
因为EF是梯形ABCD的中位线，所以EG＝
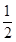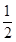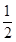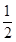CD,GF=AB，故EF=CD+AB，即AB+DC=2EF，故B正确.在四边形AEFB和四边形ABCD中，对应角相等，对应边不成比例，因此四边形AEFB和四边形ABCD不相似.故C错误；
由于EG、HF分别是△ACD、△BCD的中位线，知EG=
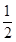CD，HF=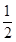CD，所以EG=FH，故D正确.故选C.
考点: 梯形的中位线.
练习册系列答案
相关题目
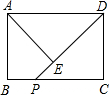
为何值时，△BPQ为直角三角形；
，则
___________.
相似且对应边上的高之比为
，若
的周长为8，则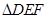
的周长为 。
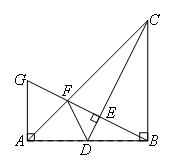
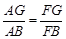；②点F是GE的中点；③AF=
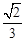AB；④S△ABC ="5" S△BDF，其中正确的结论序号是_____________．
