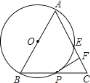
��Ŀ����
����Ŀ����ͼ��ʾ�����ɼ���С�������������ĸ���Ȧ��С�������е����ֱ�ʾ�ڸ�λ��С������ĸ�����
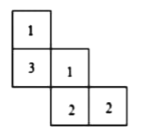
��1�����������ڻ���������ʹ����濴����������������״ͼ��
��2����ͼ����С����9���ⳤΪ1![]() ��С�������ľ��ɵļ�����ĸ���ͼ��С�������е����ֱ�ʾ�ڸ�λ��С������ĸ���������С���þ������ٵ�ͬ����С�����������Ա��ٴһ�������壬ʹС������ļ�����ǡ�ÿ��Ժ�С������ļ�����ƴ��һ����������壨��ƴ��������ʱ������һ�������巭ת���Ҽٶ����ÿ���������������ճ����һ�𣩣���
��С�������ľ��ɵļ�����ĸ���ͼ��С�������е����ֱ�ʾ�ڸ�λ��С������ĸ���������С���þ������ٵ�ͬ����С�����������Ա��ٴһ�������壬ʹС������ļ�����ǡ�ÿ��Ժ�С������ļ�����ƴ��һ����������壨��ƴ��������ʱ������һ�������巭ת���Ҽٶ����ÿ���������������ճ����һ�𣩣���
��С�����ٻ���Ҫ ��С�����壻
����������С���������ı����Ϊ ![]() ��
��
���𰸡���1������������2����18����56
��������
��1����������ͼ�Ķ��廭��ͼ�μ��ɣ�
��2���ٸ������⻭������ͼ���ɽ�����⣻
�ڸ�������ͼ�Ķ��廭��ͼ�μ��ɣ����6������ı�������ɣ�
��1����ͼ��ʾ��
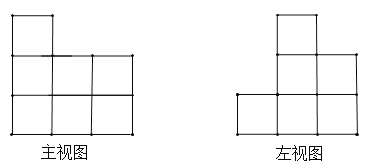
��2����ͼ�и���9�������飬��С����������Ҫ27�飬27��9=18��
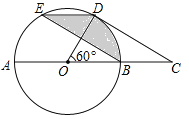
�ڸ�����֪ͼ�ο�֪����С���������ĸ���ͼ��ͼ��
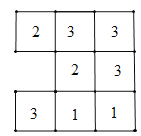
����ͼΪ9�飬����ͼΪ9�飬����ͼΪ8�飬�������9+9+8����2=52��������Ӱ���ֵ�0�飬��4����λ���ڲ����ʱ����Ϊ52+4=56��
�ʴ�Ϊ��18��56��