题目内容
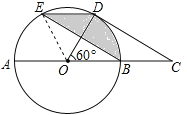
【题目】如图，在⊙O中，AB是直径，点D是⊙O上一点且∠BOD=60°，过点D作⊙O的切线CD交AB的延长线于点C，E为
的中点，连接DE，EB．
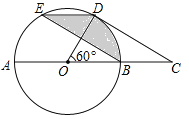
（1）求证：四边形BCDE是平行四边形；
（2）已知图中阴影部分面积为6π，求⊙O的半径r．
【答案】（1）证明见试题解析；（2）6．
【解析】试题（1）先证明DE∥BC，再由CD是⊙O的切线，得到OD⊥CD，于是得到BE∥CD，即可证得结论；
（2）连接OE，由（1）知，
，得到∠BOE=120°，根据扇形的面积公式列方程即可得到结论．
试题解析：（1）∵∠BOD=60°，∴∠AOD=120°，∴
，∵E为
的中点，∴，∴DE∥AB，OD⊥BE，即DE∥BC，∵CD是⊙O的切线，∴OD⊥CD，∴BE∥CD，∴四边形BCDE是平行四边形；
（2）连接OE，由（1）知，，∴∠BOE=120°，∵阴影部分面积为6π，∴
，∴r=6．
练习册系列答案
相关题目
