题目内容
利用图象解一元二次方程x2-2x-1=0时,我们采用的一种方法是:在直角坐标系中画出抛物线y=x2和直线y=2x+1,两图象交点的横坐标就是该方程的解.(1)请再给出一种利用图象求方程x2-2x-1=0的解的方法;
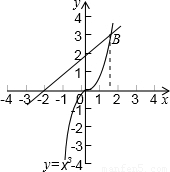
(2)已知函数y=x3的图象(如图):求方程x3-x-2=0的解.(结果保留2个有效数字)

【答案】分析:(1)由范例可得应把x2-2x-1=0进行整理,也可得到x2-1=2x,那么可得y=x2-1和y=2x两图象交点的横坐标就是该方程的解.
(2)把方程x3-x-2=0整理得x3=x+2,那么可得y=x3和y=x+2两图象交点的横坐标就是该方程的解.
解答:解:(1)方法:在直角坐标系中画出抛物线y=x2-1和直线y=2x,其交点的横坐标就是方程的解.
(2)在图中画出直线y=x+2与函数y=x3的图象交于点B,得点B的横坐标x≈1.5,
∴方程的近似解为x≈1.5.
点评:本题考查用函数图象法求解一元二次方程或一元多次方程的解,关键是把一元二次方程或一元多次方程整理为两个函数的形式.
(2)把方程x3-x-2=0整理得x3=x+2,那么可得y=x3和y=x+2两图象交点的横坐标就是该方程的解.
解答:解:(1)方法:在直角坐标系中画出抛物线y=x2-1和直线y=2x,其交点的横坐标就是方程的解.
(2)在图中画出直线y=x+2与函数y=x3的图象交于点B,得点B的横坐标x≈1.5,
∴方程的近似解为x≈1.5.

点评:本题考查用函数图象法求解一元二次方程或一元多次方程的解,关键是把一元二次方程或一元多次方程整理为两个函数的形式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 似解.(结果保留两个有效数字)
似解.(结果保留两个有效数字) 19、利用图象解一元二次方程x2-2x-1=0时,我们采用的一种方法是:在直角坐标系中画出抛物线y=x2和直线y=2x+1,两图象交点的横坐标就是该方程的解.
19、利用图象解一元二次方程x2-2x-1=0时,我们采用的一种方法是:在直角坐标系中画出抛物线y=x2和直线y=2x+1,两图象交点的横坐标就是该方程的解.

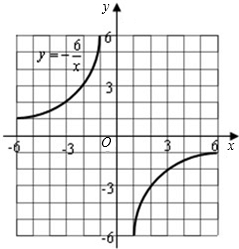
 的图象(如图所示),利用图象求方程
的图象(如图所示),利用图象求方程 -x+3=0的近似解.(结果保留两个有效数字)
-x+3=0的近似解.(结果保留两个有效数字)