Question

利用图象解一元二次方程x²+x-3=0时，我们采用的一种方法是：在平面直角坐标系中画出抛物线y=x²+x-3图象，图象与x轴交点的横坐标就是该方程的解．也可以这样求解：在平面直角坐标系中画出y=x²和直线u=-x+3，两图象交点的横坐标就是该方程的解．根据以上提示完成以下问题：

（1）在图（1）中画出函数y=x²-2x-3的图象，利用图象求方程x²-2x-3=0的解．
（2）已知函数y=-

6

x

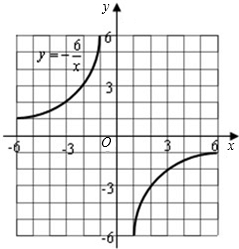
的图象（如图2所示），利用该图象求方程-x²-x+6=0的解．

Answer 1

分析：（1）建立平面直角坐标系，然后根据网格结构作出二次函数y=x²-2x-3的图象，再根据题目提供的信息找出函数图象与x轴的交点即可得解；
（2）先把方程两边都除以x，然后整理并分解成反比例函数与一次函数的形式，在图2中作出一次函数图象，然后找出两函数图象的交点坐标，从而得解．

解答：解：（1）如图1所示，建立平面直角坐标系并作出函数y=x²-2x-3的图象，
图象与x轴的交点坐标为（-1，0），（3，0），
∴方程x²-2x-3=0的解是x₁=-1，x₂=3；

（2）方程两边都除以x得，-x-1+

6

x

=0，
∴-x-1=-

6

x

，
∴函数y=-x-1与函数y=-

6

x

的交点横坐标即为方程的解，
如图2所示，交点坐标为（-3，2），（2，-3），
∴方程-x²-x+6=0的解为x₁=-3，x₂=2．

点评：本题是对二次函数的综合考查，主要是利用函数图象的交点坐标与函数图象与x轴的交点坐标求方程的解，读懂题目信息是解题的关键．