题目内容
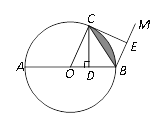
【题目】如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D, 过点B作BM∥OC,在射线BM上取点E, 使BE=BD,连接CE.
(1) 当∠COB=60° 时,直接写出阴影部分的面积;
(2) 求证:CE是 ⊙O的切线.
【答案】(1) ![]() (2)证明见解析.
(2)证明见解析.
【解析】试题分析:(1)已知∠COB=60°,CD⊥AB,OA=OB=OC=2,可求得CD=![]() ,所以
,所以![]()
![]() ;(2)根据已知条件易证△CBD≌△CBE,可得∠CEB=∠CDB=90°,再由BM∥OC可得∠OCE+∠CEB=180°,即可得∠OCE=180°-∠CEB =180°-90°=90°,结论得证.
;(2)根据已知条件易证△CBD≌△CBE,可得∠CEB=∠CDB=90°,再由BM∥OC可得∠OCE+∠CEB=180°,即可得∠OCE=180°-∠CEB =180°-90°=90°,结论得证.
试题解析:
(1) ![]()
(2)证明:∵BM∥OC
∴∠OCB=∠CBE
∵OC=OB
∴∠OCB=∠OBC
∴∠OBC=∠CBE
又BD=BE, BC=BC
∴△CBD≌△CBE
∴∠CEB=∠CDB=90°
∵BM∥OC
∴ ∠OCE+∠CEB=180°
∴∠OCE=180°-∠CEB =180°-90°=90°
即OC⊥CE ∴CE是 ⊙O的切线.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目