题目内容
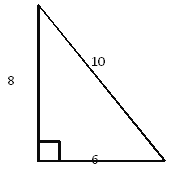
【题目】如图，已知一个边长分别为6、8、10的直角三角形，请设计出一个有一条边长为8的直角三角形，使这两个直角三角形能够拼成一个等腰三角形.
（1）画出4种不同拼法（周长不等）的等腰三角形；
（2）分别求出4种不同拼法的等腰三角形的周长.
【答案】（1）见解析；（2）见解析.
【解析】试题分析：（1）根据三角形的三边关系、勾股定理的逆定理和等腰三角形的判定来作图；
（2）利用（1）的图形，分别求得每一个等腰三角形的周长．
试题解析：（1）答案不唯一，如给出4种不同拼法，如图1-①、1-②、1-③、1-④所示.
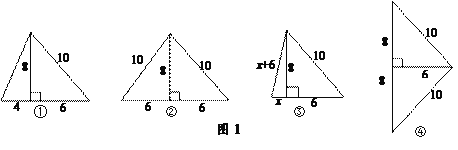
（2）如图1-①：拼成的等腰三角形的周长为10+6+4+
＝20+4
；如图1-②：拼成的等腰三角形的周长为10+10+12＝32；如图1-③：根据图示知，64+x2＝(x+6)2，解得x＝
，所以拼成的等腰三角形的周长为2×
+10＝
；如图1-④：拼成的等腰三角形的周长为10+10+8+8＝36.
练习册系列答案
阅读快车系列答案
相关题目
