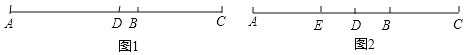题目内容
【题目】定义:P、Q分别是两条线段a,b上任意一点,线段PQ长度的最小值叫做线段a与线段b的距离.已知,O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.
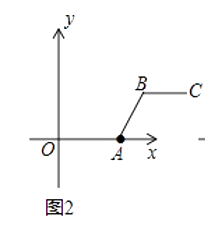
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离为;当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为;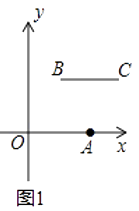
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.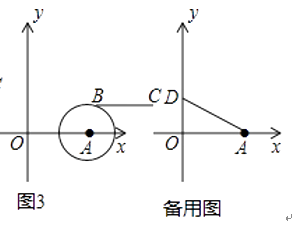
(3)当m值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,点D(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m值,使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m值;若不存在,请说明理由.
【答案】
(1)2,![]()
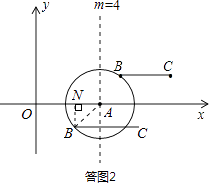
(2)解:如答图2所示,当点B落在⊙A上时,m的取值范围为2≤m≤6:
当4≤m≤6,显然线段BC与线段OA的距离等于⊙A半径,即d=2;
当2≤m<4时,作BN⊥x轴于点N,线段BC与线段OA的距离等于BN长,
ON=m,AN=OA﹣ON=4﹣m,在Rt△ABN中,由勾股定理得:
∴d= ![]() =
= ![]() =
= ![]()
(3)解:存在.
∵m≥0,n≥0,∴点M位于第一象限.
∵A(4,0),D(0,2),∴OA=2OD.
如答图4所示,相似三角形有三种情形:
(I)△AM1H1,此时点M纵坐标为2,点H在A点左侧.
如图,OH1=m+2,M1H1=2,AH1=OA﹣OH1=2﹣m,
由相似关系可知,M1H1=2AH1,即2=2(2﹣m),
∴m=1;
(II)△AM2H2,此时点M纵坐标为2,点H在A点右侧.
如图,OH2=m+2,M2H2=2,AH2=OH2﹣OA=m﹣2,
由相似关系可知,M2H2=2AH2,即2=2(m﹣2),
∴m=3;
(III)△AM3H3,此时点B落在⊙A上.
如图,OH3=m+2,AH3=OH3﹣OA=m﹣2,
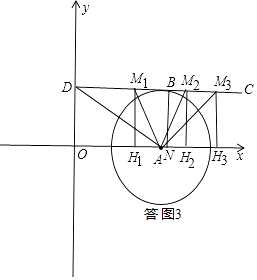
过点B作BN⊥x轴于点N,则BN=M3H3=n,AN=m﹣4,
由相似关系可知,AH3=2M3H3,即m﹣2=2n (1)
在Rt△ABN中,由勾股定理得:22=(m﹣4)2+n2 (2)
由(1)、(2)式解得:m1= ![]() ,m2=2,
,m2=2,
当m=2时,点M与点A横坐标相同,点H与点A重合,故舍去,
∴m= ![]() .
.
综上所述,存在m的值使以A、M、H为顶点的三角形与△AOD相似,m的取值为:1或3或 ![]() .
.
【解析】解:(1)当m=2,n=2时,
如题图1,线段BC与线段OA的距离(即线段BN的长)=2;
当m=5,n=2时,
B点坐标为(5,2),线段BC与线段OA的距离,即为线段AB的长,
如答图1,过点B作BN⊥x轴于点N,则AN=1,BN=2,
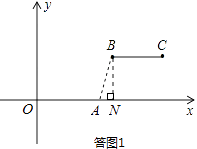
在Rt△ABN中,由勾股定理得:AB= ![]() =
= ![]() =
= ![]() ;
;
所以答案是:2, ![]() ;
;
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对点和圆的三种位置关系的理解,了解圆和点的位置关系:以点P与圆O的为例(设P是一点,则PO是点到圆心的距离),P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO<r.