题目内容
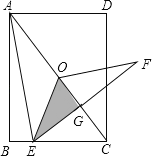
【题目】如图,矩形ABCD中,AB![]() ,BC
,BC![]() ,连结对角线AC,点O为AC的中点,点E为线段BC上的一个动点,连结OE,将△AOE沿OE翻折得到△FOE,EF与AC交于点G,若△EOG的面积等于△ACE的面积的
,连结对角线AC,点O为AC的中点,点E为线段BC上的一个动点,连结OE,将△AOE沿OE翻折得到△FOE,EF与AC交于点G,若△EOG的面积等于△ACE的面积的![]() ,则BE=_____.
,则BE=_____.
【答案】2![]()
【解析】
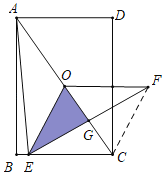
如图,连接CF.想办法证明四边形OECF是平行四边形即可解决问题.
如图,连接CF.
∵OA=OC,△EOG的面积等于△ACE的面积的![]() ,
,
∴OG=GC,
∴OA=2OG,
由翻折不变性可知:∠AEO=∠OEG,
∴![]() 2(角平分线的性质定理,可以用面积法证明),
2(角平分线的性质定理,可以用面积法证明),
∵EA=EF,
∴EG=GF,∵OG=OC,
∴四边形OECF是平行四边形,
∴OF=CE,
∵四边形ABCD是矩形,
∴∠B=90°,
∴AC![]() 2
2![]() ,
,
∴EC=OF=OA![]() ,
,
∴BE=2![]() ,
,
故答案为2![]() .
.

练习册系列答案
相关题目