题目内容
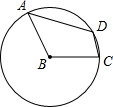 如图,若圆心角∠ABC=100°,则圆周角∠ADC=
如图,若圆心角∠ABC=100°,则圆周角∠ADC=130
130
°.分析:在优弧AEC上取点E,连接AE,CE,利用在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠E的度数,又由圆的内接四边四边形的对角互补,即可求得圆周角∠ADC的度数.
解答: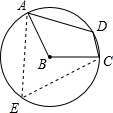 解:如图:在优弧AEC上取点E,连接AE,CE,
解:如图:在优弧AEC上取点E,连接AE,CE,
∴∠AEC=
∠ABC=
×100°=50°,
∵四边形AECD是⊙O的内接四边形,
∴∠ADC=180°-∠AEC=130°.
故答案为:130.
 解:如图:在优弧AEC上取点E,连接AE,CE,
解:如图:在优弧AEC上取点E,连接AE,CE,∴∠AEC=
| 1 |
| 2 |
| 1 |
| 2 |
∵四边形AECD是⊙O的内接四边形,
∴∠ADC=180°-∠AEC=130°.
故答案为:130.
点评:此题考查了圆周角定理与圆的内接四边形的性质.此题难度不大,解题的关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半与圆的内接四边四边形的对角互补定理的应用,注意辅助线的作法.

练习册系列答案
相关题目
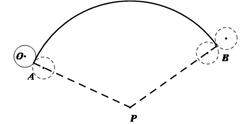
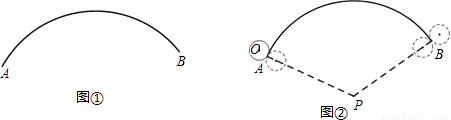
 (2013•湖州模拟)如图,若弧AB半径PA为18,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转的周数是( )
(2013•湖州模拟)如图,若弧AB半径PA为18,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转的周数是( )
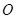 ,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙
,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙
 ,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙
,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙