Question

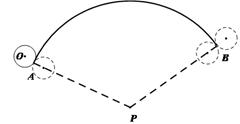
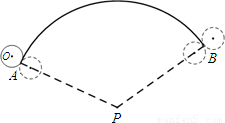
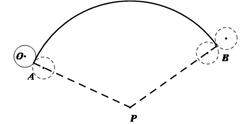
如图，若弧AB半径PA为18，圆心角为120°，半径为2的⊙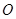，从弧AB的一个端点A（切点）开始先在外侧滚动到另一个端点B（切点），再旋转到内侧继续滚动，最后转回到初始位置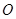，⊙自转的周数是

A．5周             B．6周　　　　      C．7周　　　        D．8周

 

Answer 1

【答案】

C

【解析】

试题分析：先根据弧长公式求得弧AB的长，再求得圆的周长公式求得⊙O的周长，即可求得⊙O滚动的长度，从而得到滚动过程中自转周数，再结合⊙O在点B出由外侧转到内侧自转180°，在点A处由内侧转到外侧自转180°，正好等于1周，即可得到结果.

弧AB的长，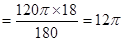

⊙O的周长=2πr=2π×2=4π，

∴⊙O滚动的长度为2×12π=24π，

滚动过程中自转周数=24π÷4π=6，

又⊙O在点B出由外侧转到内侧自转180°，在点A处由内侧转到外侧自转180°，正好等于1周，

6+1=7，

所以最后转回到初始位置，⊙O自转7周，

故选C.

考点：弧长公式，圆的周长公式

点评：解题的关键是熟练掌握弧长公式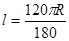：，注意在使用公式时度不带单位.