题目内容
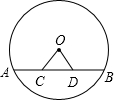
如图,⊙O的直径AB垂直于弦CD,垂足为E,AB=10,∠COD=60°,求:
(1)弦CD的长;
(2)∠COE的度数;
(3)线段BE的长(结果用根号表示).
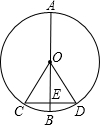
(1)弦CD的长;
(2)∠COE的度数;
(3)线段BE的长(结果用根号表示).

(1)∵半径OC=OD,即△OCD为等腰三角形,
又∵∠COD=60°,
∴△OCD为等边三角形,
∴CD=OC=
AB=5;
(2)∵直径AB垂直于弦CD于E,
∴CE=ED,
又∵OC=OD,即OE为等腰△OCD的底边CD上的高,
∴OE平分∠COD(三线合一),
∵∠COD=60°,
∴∠COE=30°;
(3)在Rt△OCE中,
∵
=cos∠COE,
∴OE=OC•cos∠COE
=5•cos30°=5•
=
,
∴BE=OB-OE=5-
.
又∵∠COD=60°,
∴△OCD为等边三角形,
∴CD=OC=
| 1 |
| 2 |
(2)∵直径AB垂直于弦CD于E,
∴CE=ED,
又∵OC=OD,即OE为等腰△OCD的底边CD上的高,
∴OE平分∠COD(三线合一),
∵∠COD=60°,
∴∠COE=30°;
(3)在Rt△OCE中,
∵
| OE |
| OC |
∴OE=OC•cos∠COE
=5•cos30°=5•
| ||
| 2 |
5
| ||
| 2 |
∴BE=OB-OE=5-
5
| ||
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目