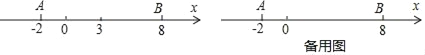Question

【题目】如图，已知是数轴上的三点，点表示的数是6，．

（1）写出数轴上点，点表示的数；

（2）点为线段的中点，，求的长；

（3）动点分别从同时出发，点以每秒6个单位长度的速度沿数轴向右匀速运动，点以每秒3个单位长度的速度沿数轴向左匀速运动，求为何值时，原点恰好为线段的中点．

Answer 1

【答案】（1）A表示的数是-10，B表示的数是2；（2）7或13；（3）当t=时，原点O为PQ的中点

【解析】

（1）根据点C表示的数和B,C之间的距离可求出B表示的数，然后再根据A,B之间的距离即可求出A表示的数；

（2）根据M是AB的中点，求出BM的长度，然后分N点在C的左侧和右侧两种情况，当N在C左侧时，BN=BC-CN，当N在C右侧时，BN=BC+CN，最后利用MN=BM+BN即可得出答案；

（3）原点O为PQ的中点时，OP=OQ,分别用含t的代数式表示出OP,OQ，然后建立方程，解方程即可求出t的值．

∵点表示的数是6，

∴点B表示的数为

∴点A表示的数为

∴A表示的数是-10，B表示的数是2 ．

(2) ∵AB＝12，M是AB的中点．

∴AM=BM=6，

∵CN=3

当点N在点C的左侧时，BN=BC-CN=1，此时MN=BM+BN=6+1=7

当点N在点C的右侧时，BN=BC+CN=7，此时MN=BM+BN=6+9=13

综上所述，MN的值为7或13

（3）∵A表示的数是-10，即OA=10

C表示的数是6，即OC=6

又∵点P、点Q同时出发，且运动的时间为t

∴AP=6t，CQ=3t，

∴OP=OA-AP=10-6t，OQ=OC-CQ=6-3t

当原点O为PQ的中点时，OP=OQ

∴ 10-6t=6-3t．

解得t=

∴当t=时，原点O为PQ的中点．