��Ŀ����
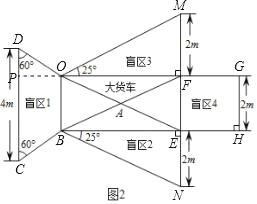
����Ŀ����ͼ1��ijѧУ��չ����ͨ��ȫ�ա�����ڻ�У�����������ͬѧ��չʾ�˴����ä���ķֲ�����������Ѵ�ң����ڼ�ʻ�ҵ�˾��������������ä���е�ͬѧ�ǣ�����һ��ҪԶ��������ä��������������ȫ��С�����ڵ�ѧϰС��Ϊ�˸��õķ��������ä�������⣬��ͼ1��ƽ��ͼ�ν��б�ʾ������ע�˲����������ݣ���ͼ2����ͼ2�д��������״Ϊ���Σ���ä��1Ϊ���Σ�ä��2��ä��3Ϊֱ�������Σ�ä��4Ϊ�����Σ�
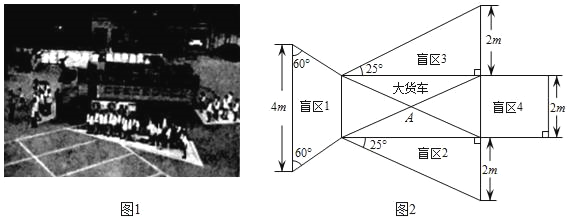
�������С�յ�ѧϰС������������⣺
��1��ä��1�����Լ�Ƕ���m2��ä��2�����Լ�Ƕ���m2��
��![]() ��1.4��
��1.4��![]() ��1.7��sin25���0.4��cos25���0.9��tan25���05���������������
��1.7��sin25���0.4��cos25���0.9��tan25���05���������������
��2������Դ����������A��ΪԲ�ģ���������ä���İ뾶��С��ԲΪ�������Σ����������ͼ2�л����������Σ������
���𰸡���1��ä��1�����Լ��5m2��ä��2�����Լ��4m2����2����AΪԲ�ģ�AC��Ϊ�뾶������ԲΪ�������Σ��������ͼ��ʾ������.
��������
��1����OP��CD��P�����ݵ������ε��������DP��![]() ��CD��OB����1����ֱ�ǡ�ODP���ó�OP��DPtan��D��
��CD��OB����1����ֱ�ǡ�ODP���ó�OP��DPtan��D��![]() �����������ε������ʽ�������ä��1���������ֱ�ǡ�BEN�����BE��
�����������ε������ʽ�������ä��1���������ֱ�ǡ�BEN�����BE��![]() ��4����ôS��BEN��
��4����ôS��BEN��![]() BEEN��4m2����Ϊä��2�������
BEEN��4m2����Ϊä��2�������
��2�����ù��ɶ������AC��AD��![]() ��
��![]() ��AH��AG��
��AH��AG��![]() ��
��![]() ��AM��AN��
��AM��AN��![]() ��
��![]() ���õ�AC�����ô��AΪԲ�ģ�AC��Ϊ�뾶������ԲΪ�������Σ������
���õ�AC�����ô��AΪԲ�ģ�AC��Ϊ�뾶������ԲΪ�������Σ������
��1����ͼ����OP��CD��P��
��OBCD�ǵ������Σ�OB��2��CD��4��
��DP��![]() ��CD��OB����1��
��CD��OB����1��
��ֱ�ǡ�ODP�У��ߡ�D��60�㣬
��OP��DPtan��D��1��![]() ��
��![]() ��
��
��S����OBCD��![]() ��OB+CD��OP��
��OB+CD��OP��![]() ��2+4��
��2+4��![]() ��3
��3![]() ��3��1.7��5��m2����
��3��1.7��5��m2����
��ä��1�����Լ��5m2��
��ֱ�ǡ�BEN�У��ߡ�EBN��25�㣬EN��2��
��BE��![]() ��4��
��4��
��S��BEN��![]() BEEN��
BEEN��![]() ��4��2��4��m2����
��4��2��4��m2����
��ä��2�����Լ��4m2��
�ʴ�Ϊ5��4��
��2����AC��AD��![]() ��
��
AH��AG��![]() ��
��
AM��AN��![]() ��
��
��AC��AD��AH��AG��AM��AN��
����AΪԲ�ģ�AC��Ϊ�뾶������ԲΪ�������Σ������
��ͼ��ʾ��

 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�