题目内容
【题目】在矩形ABCD中,AB=3,BC=6,P为BC边上一点,△APD为等腰三角形.
(1)小明画出了一个满足条件的△APD,其中PA=PD,如图1所示,则tan ![]() 的值为 ;
的值为 ;
(2)请你在图2中再画出一个满足条件的△APD(与小明的不同),并求此时tan ![]() 的值.
的值.
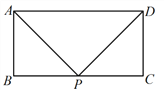

图1 图2
【答案】(1)1(2)![]()
【解析】试题分析:
(1)由全等三角形求出BP=CP=3,由三角函数定义即可得出结果;
(2)分两种情况:①AP=AD=6;PD=AD=6时;由三角函数定义即可得出结果.
试题解析:
解:(1)∵四边形ABCD是矩形,
∴AB=DC,∠B=∠C=90°,
∵PA=PD,
∴△ABP≌△DCP(HL)
∴BP=CP=![]() BC=3,
BC=3,
∴tan∠BAP=![]() =
=![]() =1.
=1.
故答案为:1;
(2)分两种情况:
①如图1:
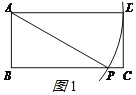
AP=AD=6时,BP=![]() =
=![]() =
=![]() ,
,
∴tan∠BAP=![]() =
=![]() =
=![]() ;
;
②如图2:
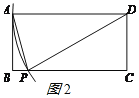
PD=AD=6时,CP=![]() =
=![]() =
=![]() ,
,
∴BP=BC-CP=6-![]() ,
,
∴tan∠BAP=![]() =
=![]() =2-
=2-![]() .
.

练习册系列答案
相关题目