Question

【题目】综合题。
（1）证明：“三角形内角和是180°”；
（2）请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题，判断这一逆命题是真命题还是假命题，如果是真命题给出证明，如果是假命题，说明理由．

Answer 1

【答案】
（1）证明：已知：△ABC，

求证：∠BAC+∠B+∠C=180°，

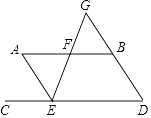
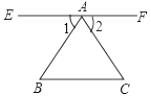
证明：过点A作EF∥BC，

∵EF∥BC，

∴∠1=∠B，∠2=∠C，

∵∠1+∠2+∠BAC=180°，

∴∠BAC+∠B+∠C=180°．

即知三角形内角和等于180°

（2）解：“直角三角形斜边上的中线等于斜边的一半”的逆命题是一个三角形一边上的中线是这边的一半，那么这个三角形是直角三角形，是真命题．

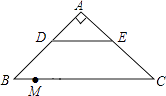
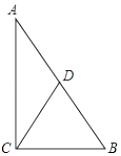
已知，如图，△ABC中，D是AB边的中点，且CD= AB

求证：△ABC是直角三角形，

证明：∵D是AB边的中点，且CD= AB，

∴AD=BD=CD，

∵AD=CD，

∴∠ACD=∠A，

∵BD=CD，

∴∠BCD=∠B，

又∵∠ACD+∠BCD+∠A+∠B=180°，

∴2（∠ACD+∠BCD）=180°，

∴∠ACD+∠BCD=90°，

∴∠ACB=90°，

∴△ABC是直角三角形．

【解析】（1）根据平行线的性质、平角的定义证明；（2）根据等腰三角形的性质、三角形内角和定理证明．
【考点精析】通过灵活运用命题与定理，掌握我们把题设、结论正好相反的两个命题叫做互逆命题．如果把其中一个叫做原命题，那么另一个叫做它的逆命题；经过证明被确认正确的命题叫做定理即可以解答此题．