题目内容
【题目】如图AB∥CD,EF分别交AB于点F,交CD于点E,EF与DB交于点G,且EA平分∠CEF,∠BFG=70°.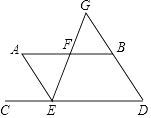
(1)求∠A的度数.
(2)若∠A=∠D,求证:∠AEF=∠G.
【答案】
(1)解:∵∠AFE=∠BFG=70°,
∵AB∥CD,
∴∠CEF=180°﹣∠AFE=110°,
∵且EA平分∠CEF,
∴∠AEF= ![]() CEF=55°,
CEF=55°,
∴∠A=180°﹣∠AFE﹣∠AEF=55°
(2)解:∵AB∥CD,
∴∠GED=∠GFB=70°,
∵∠D=∠A=55°,
∴∠G=55°,
∴∠AEF=∠G
【解析】(1)由AB∥CD可得同旁内角互补,即∠CEF=180°﹣∠AFE=110°,由EA平分∠CEF,∠A可转化为∠ AEC,即可求出;(2)由(1)∠AEF=∠A,可求出∠G=55°,即∠AEF=∠G.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目