ЬтФПФкШн
ЁОЬтФПЁПдФЖСНтД№ЬтЃК
ЃЈМИКЮИХаЭЃЉ
ЬѕМўЃКШчЭМ1ЃК![]() ЪЧжБЯп
ЪЧжБЯп![]() ЭЌХдЕФСНИіЖЈЕуЃЎ
ЭЌХдЕФСНИіЖЈЕуЃЎ
ЮЪЬтЃКдкжБЯп![]() ЩЯШЗЖЈвЛЕу
ЩЯШЗЖЈвЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФжЕзюаЁЃЛ
ЕФжЕзюаЁЃЛ
ЗНЗЈЃКзїЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЖдГЦЕу
ЖдГЦЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ,
,
гЩЁАСНЕужЎМфЃЌЯпЖЮзюЖЬЁБПЩжЊЃЌЕу![]() МДЮЊЫљЧѓЕФЕуЃЎ
МДЮЊЫљЧѓЕФЕуЃЎ
ЃЈФЃаЭгІгУЃЉ
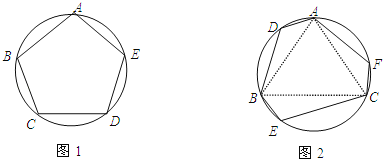
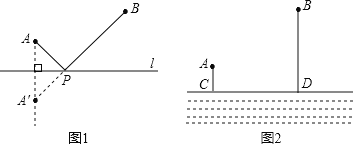
ШчЭМ2ЫљЪОЃКСНДх![]() дквЛЬѕКг
дквЛЬѕКг![]() ЕФЭЌВрЃЌ
ЕФЭЌВрЃЌ![]() СНДхЕНКгБп
СНДхЕНКгБп![]() ЕФОрРыЗжБ№ЪЧ
ЕФОрРыЗжБ№ЪЧ![]() ЧЇУз,
ЧЇУз,![]() ЧЇУз,
ЧЇУз, ![]() ЧЇУзЃЌЯжвЊдкКгБп
ЧЇУзЃЌЯжвЊдкКгБп![]() ЩЯНЈдьвЛЫЎГЇЃЌЯђ
ЩЯНЈдьвЛЫЎГЇЃЌЯђ![]() СНДхЫЭЫЎЃЌЦЬЩшЫЎЙмЕФЙЄГЬЗбгУЮЊУПЧЇУз20000дЊЃЌЧыФудк
СНДхЫЭЫЎЃЌЦЬЩшЫЎЙмЕФЙЄГЬЗбгУЮЊУПЧЇУз20000дЊЃЌЧыФудк![]() ЩЯбЁдёЫЎГЇЮЛжУЃЌЪЙЦЬЩшЫЎЙмЕФЗбгУзюЪЁЃЌВЂЧѓГізюЪЁЕФЦЬЩшЫЎЙмЕФЗбгУ
ЩЯбЁдёЫЎГЇЮЛжУЃЌЪЙЦЬЩшЫЎЙмЕФЗбгУзюЪЁЃЌВЂЧѓГізюЪЁЕФЦЬЩшЫЎЙмЕФЗбгУ![]() ЃЎ
ЃЎ
ЃЈЭиеЙбгЩьЃЉ
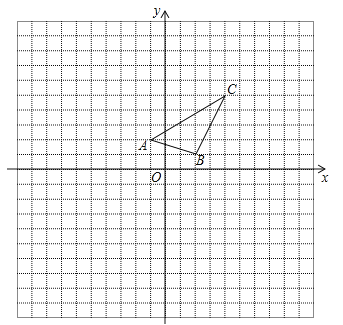
ШчЭМЃЌ![]() жаЃЌЕу
жаЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌЙ§
ЩЯЃЌЙ§![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЩЯвЛИіЖЏЕуЃЌСЌНг
ЩЯвЛИіЖЏЕуЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() зюаЁЃЌдђЕу
зюаЁЃЌдђЕу![]() гІИУТњзуЃЈ ЃЉЃЈЮЈвЛбЁЯюе§ШЗЃЉ
гІИУТњзуЃЈ ЃЉЃЈЮЈвЛбЁЯюе§ШЗЃЉ
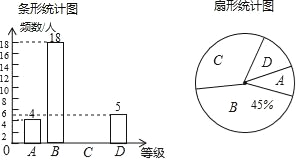
AЃЎ ![]() BЃЎ
BЃЎ ![]()
CЃЎ ![]() DЃЎ
DЃЎ ![]()
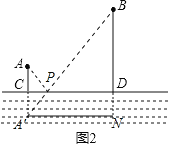
ЁОД№АИЁПЁОФЃаЭгІгУЁПЭММћНтЮіЃЌзюЪЁЕФЦЬЩшЙмЕРЗбгУЪЧ10000дЊЃЛЁОЭиеЙбгЩьЁПD
ЁОНтЮіЁП
1.ЁОФЃаЭгІгУЁПгЩгкЦЬЩшЫЎЙмЕФЙЄГЬЗбгУЮЊУПЧЇУз15000дЊЃЌЪЧвЛИіЖЈжЕЃЌЯждквЊдкCDЩЯбЁдёЫЎГЇЮЛжУЃЌЪЙЦЬЩшЫЎЙмЕФЗбгУзюЪЁЃЌвтЫМЪЧдкCDЩЯеввЛЕуPЃЌЪЙAPгыBPЕФКЭзюаЁЃЌЩш![]() ЪЧAЕФЖдГЦЕуЃЌЪЙAP+BPзюЖЬОЭЪЧЪЙ
ЪЧAЕФЖдГЦЕуЃЌЪЙAP+BPзюЖЬОЭЪЧЪЙ![]() зюЖЬЃЎ
зюЖЬЃЎ
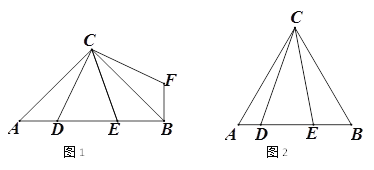
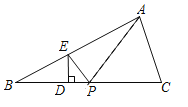
2.ЁОЭиеЙбгЩьЁПзїЕуEЙигкжБЯпBCЕФЖдГЦЕуFЃЌСЌНгAFНЛBCгкPЃЌДЫЪБPA+PEЕФжЕзюаЁЃЌвРОнжсЖдГЦЕФаджЪМДПЩЕУЕНЁЯAPC=ЁЯDPEЃЎ
1.ЁОФЃаЭгІгУЁП
ШчЭМЫљЪОЃЎбгГЄ![]() ЕН
ЕН![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ,
,
Еу![]() ОЭЪЧЫљбЁдёЕФЮЛжУЃЎ
ОЭЪЧЫљбЁдёЕФЮЛжУЃЎ
Й§![]() зї
зї![]() НЛ
НЛ![]() бгГЄЯпгкЕу
бгГЄЯпгкЕу![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрЫФБпаЮ![]() ЪЧОиаЮЃЌ
ЪЧОиаЮЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дкжБНЧШ§НЧаЮ![]() жа,
жа, ![]() ,
,
![]() ЧЇУзЃЌ
ЧЇУзЃЌ
ЁрзюЖЬТЗЯп![]() ЧЇУзЃЌ
ЧЇУзЃЌ
зюЪЁЕФЦЬЩшЙмЕРЗбгУЪЧ![]() (дЊ)ЃЎ
(дЊ)ЃЎ
2.ЁОЭиеЙбгЩьЁП
ШчЭМЃЌзїЕуEЙигкжБЯпBCЕФЖдГЦЕуFЃЌСЌНгAFНЛBCгкPЃЌДЫЪБPA+PEЕФжЕзюаЁЃЎ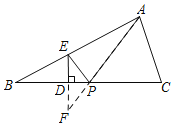
гЩЖдГЦадПЩжЊЃКЁЯDPE=ЁЯFPDЃЌ
ЁпЁЯAPC=ЁЯFPDЃЌ
ЁрЁЯAPC=ЁЯDPEЃЌ
ЁрPA+PEзюаЁЪБЃЌЕуPгІИУТњзуЁЯAPC=ЁЯDPEЃЌ
ЙЪбЁЃКDЃЎ

 вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ
вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИЁОЬтФПЁППЦЛУаЁЫЕЁЖЪЕбщЪвЕФЙЪЪТЁЗжаЃЌгаетбљвЛИіЧщНкЃЌПЦбЇМвАбвЛжжефЦцЕФжВЮяЗжБ№ЗХдкВЛЭЌЮТЖШЕФЛЗОГжаЃЌОЙ§вЛЖЮЪБМфКѓЃЌМЧТМЯТетжжжВЮяИпЖШЕФдіГЄЧщПіЃЈШчЯТБэЃЉЃК
ЮТЖШx/Ёц | Ё | Љ4 | Љ2 | 0 | 2 | 4 | 6 | Ё |
жВЮяУПЬьИпЖШЕФдіГЄСПy/mm | Ё | 41 | 49 | 49 | 41 | 25 | 1 | Ё |
гЩетаЉЪ§ОнЃЌПЦбЇМвЭЦВтГіжВЮяУПЬьИпЖШЕФдіГЄСПyЪЧЮТЖШxЕФЖўДЮКЏЪ§ЃЌФЧУДЯТСаШ§ИіНсТлЃК
ЂйИУжВЮядк0ЁцЪБЃЌУПЬьИпЖШЕФдіГЄСПзюДѓЃЛ
ЂкИУжВЮядкЉ6ЁцЪБЃЌУПЬьИпЖШЕФдіГЄСПФмБЃГждк25mmзѓгвЃЛ
ЂлИУжВЮягыДѓЖрЪ§жВЮяВЛЭЌЃЌ6ЁцвдЩЯЕФЛЗОГЯТИпЖШМИКѕВЛдіГЄ.
ЩЯЪіНсТлжаЃЌЫљгае§ШЗНсТлЕФађКХЪЧ
A. ЂйЂкЂл B. ЂйЂл C. ЂйЂк D. ЂкЂл