��Ŀ����
����Ŀ����P����dֵ���������£�����QΪԲ������һ�㣬�߶�PQ���ȵ����ֵ����Сֵ֮�Ϊ��P����dֵ������ΪdP���ر�ģ�����P��Q�غ�ʱ���߶�PQ�ij���Ϊ0������O�İ뾶Ϊ2ʱ��
��1������C����![]() ��0����D��3��4������dc=�� ����dp=�� ����
��0����D��3��4������dc=�� ����dp=�� ����
��2������ֱ��y=2x+2�ϴ��ڵ�P��ʹ��dP=2�������P�ĺ����ꣻ
��3��ֱ��y=��![]() x+b��b��0����x�ᣬy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ��2��dP��3������ֱ��д��b��ȡֵ��Χ��
x+b��b��0����x�ᣬy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ��2��dP��3������ֱ��д��b��ȡֵ��Χ��
���𰸡���1��1��4����2��P�ĺ�����Ϊ��1��![]() ����3��
����3��![]() ��b��
��b��![]() ��
��
��������
��1��Բ�ڵĵ��dֵ=����㵽Բ�ľ����2����Բ�ϻ�Բ��ĵ��dֵ=Բ��ֱ�����ɴ˼��ɽ�����⣻
��2���������⣬����dp=2�ĵ�λ�ڡ�O�ڲ���������OΪԲ�İ뾶Ϊ1��Բ�ϣ����Լ���P��a��2a+2��������PO=1���������̼��ɽ�����⣻
��3���������⣬����2��dP��3�ĵ�λ�ڵ�OΪԲ���⾶Ϊ![]() ���ھ�Ϊ1��Բ���ڣ��ֲ������Բ���߶�AB����ʱb��ֵ���ɽ�����⣻
���ھ�Ϊ1��Բ���ڣ��ֲ������Բ���߶�AB����ʱb��ֵ���ɽ�����⣻
�⣺��1����������ɵ�Բ�ڵĵ��dֵ=����㵽Բ�ľ����2����Բ�ϻ�Բ��ĵ��dֵ=Բ��ֱ��������dc=1��dp=4��
�ʴ�Ϊ1��4��
��2���������⣬����dp=2�ĵ�λ����O�ڲ���������OΪԲ�İ뾶Ϊ1��Բ�ϣ�
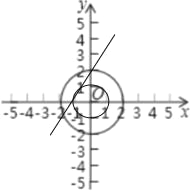
����P��ֱ��y=2x+2�ϣ������Լ���P��a��2a+2����
��PO=1��
��a2+��2a+2��2=1��
���a=��1��![]() ��
��
�����������ĵ�P�ĺ�����Ϊ��1��![]() ��
��
��3���������⣬����2��dP��3�ĵ�λ�ڵ�OΪԲ���⾶Ϊ![]() ���ھ�Ϊ1��Բ���ڣ�
���ھ�Ϊ1��Բ���ڣ�
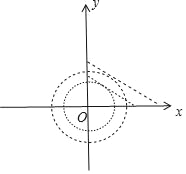
���߶��������ʱ���ɵ�b=![]() ��
��
���߶����ڻ�����ʱ���ɵ�b=![]() ��
��
��������������b��ֵ��![]() ��b��
��b��![]() ��
��

 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�