题目内容
【题目】已知直线l1:y=k1x+b1,l2:y=k2x+b2,当l1⊥l2时,有k1k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,则k=______;
(2)一直线经过点(2,3),且与直线![]() 垂直,求该直线的解析式.
垂直,求该直线的解析式.
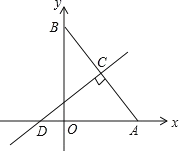
(3)如图,在平面直角坐标系中,已知Rt△AOB的两边OA、OB分别在x轴,y轴的正半轴上,且OA=6,OB=8,求线段AB的垂直平分线CD的解析式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由y=2x+1与y=kx-1垂直可得出2k=-1,解之即可得出结论;
(2)设直线l解析式为y=ax+b,根据直线l与直线y=-![]() x+3垂直可得出-
x+3垂直可得出-![]() a=-1,解之即可得出a值,再根据点A的坐标利用待定系数法即可求出直线l解析式;
a=-1,解之即可得出a值,再根据点A的坐标利用待定系数法即可求出直线l解析式;
(3)根据OA、OB的长度可得出点A、B的坐标,利用待定系数法即可求出直线AB的解析式,由点C为线段AB的中点可得出点C的坐标,根据AB⊥直线CD可求出直线CD解析式一次项系数,再根据点C的坐标利用待定系数法即可求出直线CD的解析式.
(1)∵y=2x+1与y=kx-1垂直,
∴2k=-1,
解得:k=-![]() .
.
故答案为:-![]() ;
;
(2)设直线l解析式为y=ax+b,
∵直线l与直线y=-![]() x+3垂直,
x+3垂直,
∴-![]() a=-1,
a=-1,
解得:a=3,
将A(2,3)代入y=3x+b,
3=3×2+b,解得:b=-3,
∴直线l解析式为y=3x-3;
(3)∵Rt△AOB的两直角边OA、OB分别在x轴,y轴的正半轴上,且OA=6,OB=8,
∴点A(6,0),点B(0,8),
又∵点C为线段AB的中点,
∴点C(3,4),
设直线AB的解析式为y1=k1x+b1,直线CD的解析式为y2=k2x+b2,
将点A(6,0)、B(0,8)代入y1=k1x+b1,
得![]() ,
,
解得: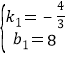 ,
,
∴直线AB的解析式为y=-![]() x+8,
x+8,
∵直线AB⊥直线CD,
∴k1k2=-1,
∴k2=![]() ,
,
将点C(3,4)代入y2=![]() x+b2,得4=
x+b2,得4=![]() ×3+b2,
×3+b2,
解得:b2=![]() ,
,
∴直线CD的解析式为y=![]() x+
x+![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】我校为了迎接体育中考,了解学生的体育成绩,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:
成绩段 | 频数 | 频率 |
160≤x<170 | 5 | 0.1 |
170≤x<180 | 10 | a |
180≤x<190 | b | 0.14 |
190≤x<200 | 16 | c |
200≤x<210 | 12 | 0.24 |
表(1)
根据图表解决下列问题:
(1)本次共抽取了多少名学生进行体育测试,表(1)中,a、b、c分别等于多少?
(2)补全图(2),所抽取学生成绩中中位数在哪个分数段;
(3)“跳绳”数在180以上,则此项成绩可得满分.那么,你估计全校九年级有多少学生在此项成绩中获满分?