题目内容
【题目】如图,在正方形网格中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题:
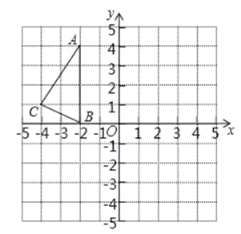
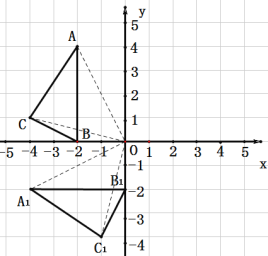
(1)将△ABC绕O点逆时针旋转90°,得到△A1B1C1;
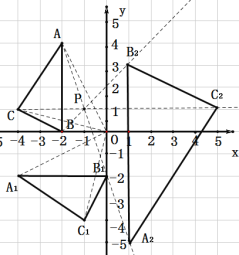
(2)以点P(-1,1)为位似中心,在△ABC的异侧作位似变换,且使△ABC的面积扩大为原来的4倍,得到△A2B2C2,并写出点A2的坐标.
【答案】(1)作图见解析(2)作图见解析,点A2的坐标为:(1,-5)
【解析】
(1)根据旋转的意义,分别连接OA、OB、OC,将它们绕点O分别逆时针旋转90°即可.
(2)根据相似的性质,得出两图形的相似比,相似比即为位似比,然后根据位似的作图方法进行位似作图即可.通过观察图形即可确定A2的坐标.
解:(1)分别连接OA、OB、OC
将OA、OB、OC分别以点O为旋转中心,逆时针旋转90°,到![]() ,连接
,连接![]() ,如图所示:△A1B1C1,即为所求;
,如图所示:△A1B1C1,即为所求;
(2)根据相似的性质,面积之比等于相似比的平方,可知变换后的图形与三角形ABC相似,且相似比为![]() ,位似比等于相似比,连接AP并延长AP到
,位似比等于相似比,连接AP并延长AP到![]() ,使
,使![]() =2AP,连接CP并延长CP到
=2AP,连接CP并延长CP到![]() ,使
,使![]() =2CP,连接BP,并延长BP至
=2CP,连接BP,并延长BP至![]() ,使
,使![]() ,连接
,连接![]() 如图所示:△A2B2C2,即为所求,由图可知:点A2的坐标为:(1,-5).
如图所示:△A2B2C2,即为所求,由图可知:点A2的坐标为:(1,-5).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目