题目内容
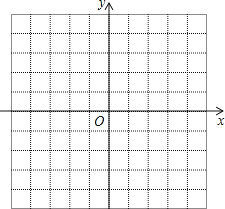
【题目】如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度,在第二象限内有横、纵坐标均为整数的A、B两点,点B(﹣2,3),点A的横坐标为﹣2,且OA= ![]() .
. 
(1)直接写出A点的坐标,并连接AB,AO,BO;
(2)画出△OAB关于点O成中心对称的图形△OA1B1 , 并写出点A1、B1的坐标;(点A1、B1的对应点分别为A、B)
(3)将△OAB水平向右平移4个单位长度,画出平移后的△O1A2B2 .
【答案】
(1)
解:A(﹣2,1)
(2)
解:△OA1B1如图所示;

A1(2,﹣1),B1(2,﹣3)
(3)
解:△O1A2B2如图所示.

【解析】(1)根据平面直角坐标系找出点B的位置,再根据勾股定理确定出点A的位置,然后顺次连接即可;(2)根据网格结构找出点A、B关于原点O的对应点A1、B1的位置,然后与点O顺次连接,再根据平面直角坐标系写出各点的坐标;(3)根据平面直角坐标系找出点O、A、B平移后的对应点O1、B2、C2的位置,然后顺次连接即可.

练习册系列答案
相关题目






