题目内容
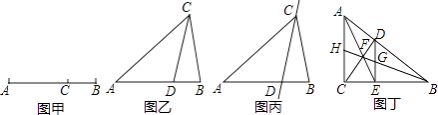
【题目】如图①,数轴上的点A、B分别表示数a、b,则点A、B(点B在点A的右侧)之间的距离表示为AB=b﹣a,若点C对应的数为c,满足|a+3|+(c﹣9)2=0.
(1)写出AC的值 .
(2)如图②,点D在点C的右侧且距离m(m>0)个单位,点B在线段AC上,满足AB+AC=BD,求AB的值(用含有m的代数式表示).
(3)如图③,若点D在点C的右侧6个单位处,点P从点A出发以2个单位/秒的速度向右运动,同时点M从点C出发以1个单位/秒的速度也向右运动,当到达D点后以原来的速度向相反的方向运动.求经过多长时间,点P和点M之间的距离是2个单位?

【答案】(1)12;(2)AB=![]() m;(3)
m;(3)![]() 或
或![]() .
.
【解析】
(1)利用非负数的性质求出a,c的值即可解决问题.
(2)由AB+AC=BD,推出AB+AB+BC=BC+CD,推出2AB=CD=m,即可解决问题.
(3)设经过x秒点P和点M之间的距离是2个单位.分两种情形构建方程即可解决问题.
解:(1)∵|a+3|+(c﹣9)2=0,
又∵|a+3|≥0,(c﹣9)2≥0,
∴a=﹣3,c=9,
∴AC=9﹣(﹣3)=12,
故答案为12.
(2)∵AB+AC=BD,
∴AB+AB+BC=BC+CD,
∴2AB=CD=m,
∴AB=![]() m.
m.
(3)设经过x秒点P和点M之间的距离是2个单位.
由题意:18﹣(2t+t﹣6)=2或(2t+t﹣6)﹣18=2,
解得t=![]() 或
或![]() .
.
∴经过![]() 或
或![]() 秒点P和点M之间的距离是2个单位.
秒点P和点M之间的距离是2个单位.

练习册系列答案
相关题目