题目内容
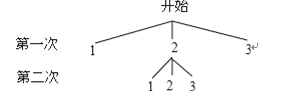
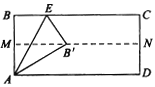
【题目】如图所示,将矩形ABCD纸对折,设折痕为MN,再把B点叠在折痕线MN上,(如图点B’),若![]() ,则折痕AE的长为( )
,则折痕AE的长为( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
【答案】C
【解析】
先作辅助线,然后根据折叠的性质和解直角三角形计算.
延长EB′与AD交于点F,
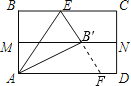
∵∠AB′E=∠B=90°,MN是对折折痕,
∴EB′=FB′,∠AB′E=∠AB′F,
在△AEB′和△AFB′中,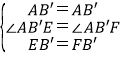 ,
,
∴△AEB′≌△AFB′,
∴AE=AF,
∴∠B′AE=∠B′AD(等腰三角形三线合一),
故根据题意,易得∠BAE=∠B′AE=∠B′AD;
故∠EAB=30°,
∴EB=![]() EA,
EA,
设EB=x,AE=2x,
∴(2x)2=x2+AB2,x=1,
∴AE=2,
则折痕AE=2,
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目